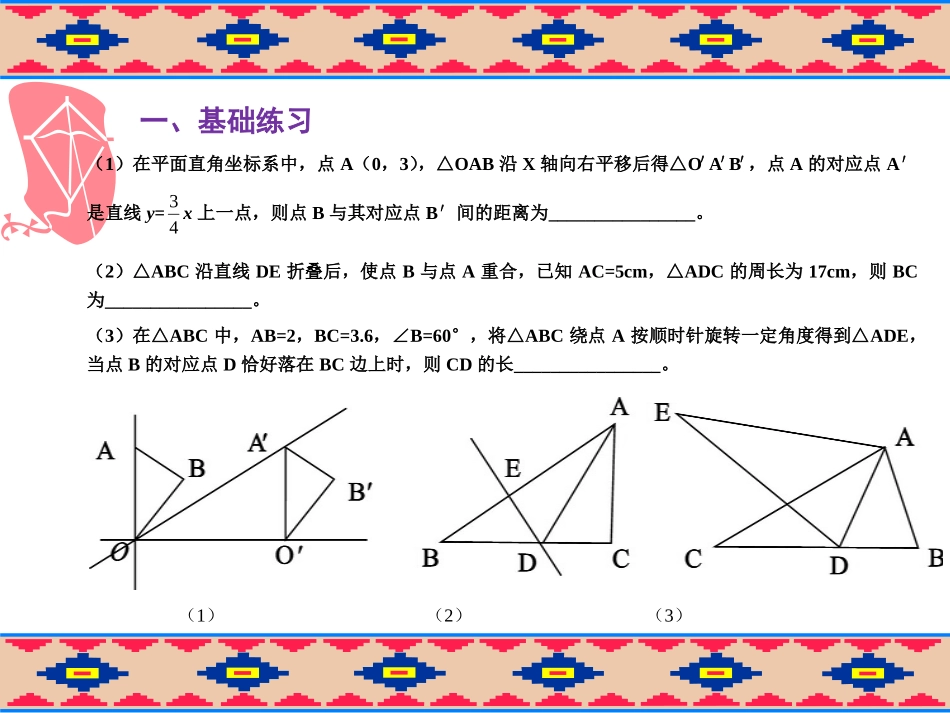
图形的轴对称、平移、旋转通州区平潮实验中学数学组Tuxingdezhouduichen、pingyi、xuanzhuan一、基础练习(1)在平面直角坐标系中,点A(0,3),△OAB沿X轴向右平移后得△O′A′B′,点A的对应点A′是直线y=43x上一点,则点B与其对应点B′间的距离为________________。(2)△ABC沿直线DE折叠后,使点B与点A重合,已知AC=5cm,△ADC的周长为17cm,则BC为________________。(3)在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长________________。(1)(2)(3)二、典型例题例1、在直角坐标系中,A(3,4)B(2,5)C(6,8),且以A、B、C、D为顶点的四边形是平行四边形,求点D的坐标(3,4)(6,8)(2,5)二、典型例题例2、问题背景,如图(1)点A、B在直线l的同侧,要在l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连结AB′与直线l交于点C,则点C即为所求。(1)二、典型例题如图2,已知⊙O的直径CD为4,点A在⊙O上,∠ACD=30°,B为AD的中点,P为直径CD上一动点,求BP+AP的最小值。(2)(1)实践应用二、典型例题(1)实践应用如图3,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(21,0),点P为斜边OB上的动点,求APC周长的最小值。(3)二、典型例题(2)知识拓展在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交AC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值。二、典型例题例3、将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°(1)将图①中△A1B1C顺时针旋转45°得图②,点Q是A1B1与BC的交点,求证CP1=CQ(2)在(1)的条件下,若AP1=2,求CQ(3)如图③在B1C上取一点E,连BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值。二、典型例题例3、将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°变式:(4)若△A1CB1以C为旋转中心,顺时针旋转α,求当α为何值时,△A1P1A是等腰三角形二、典型例题例3、将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°变式:(5)若BC=1,点P是A1B1的中点,M是BC的中点,在旋转的过程中,求PM的最大值和最小值ACB1BA1PM(5)谢谢!三、课后练习1、如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对应点F恰好落在BC上,已知折痕AE=105cm,且tan∠EFC=43,那么该矩形的周长为_____.2、已知EF为矩形ABCD的AB、BC的两个动点,把△BEF沿EF对折得△GEF,已知AD=4,DC=3,则AG的最小值为_______.三、课后练习3、如图①在正方形ABCD中,△AEF的顶点E、F分别在BC、CD边上,高AG与正方形的边长相等,求∠EAF的度数。(2)如图②在Rt△ABD中,∠BAD=90°,AB=AD,点M、N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH的位置,连结NH,试判断MN、ND、BM之间的数量关系,并说明理由。(3)在图①中,连结BD分别交AE、AF于点MN,若EG=4、GF=6,BM=32,求AG、MN的长。