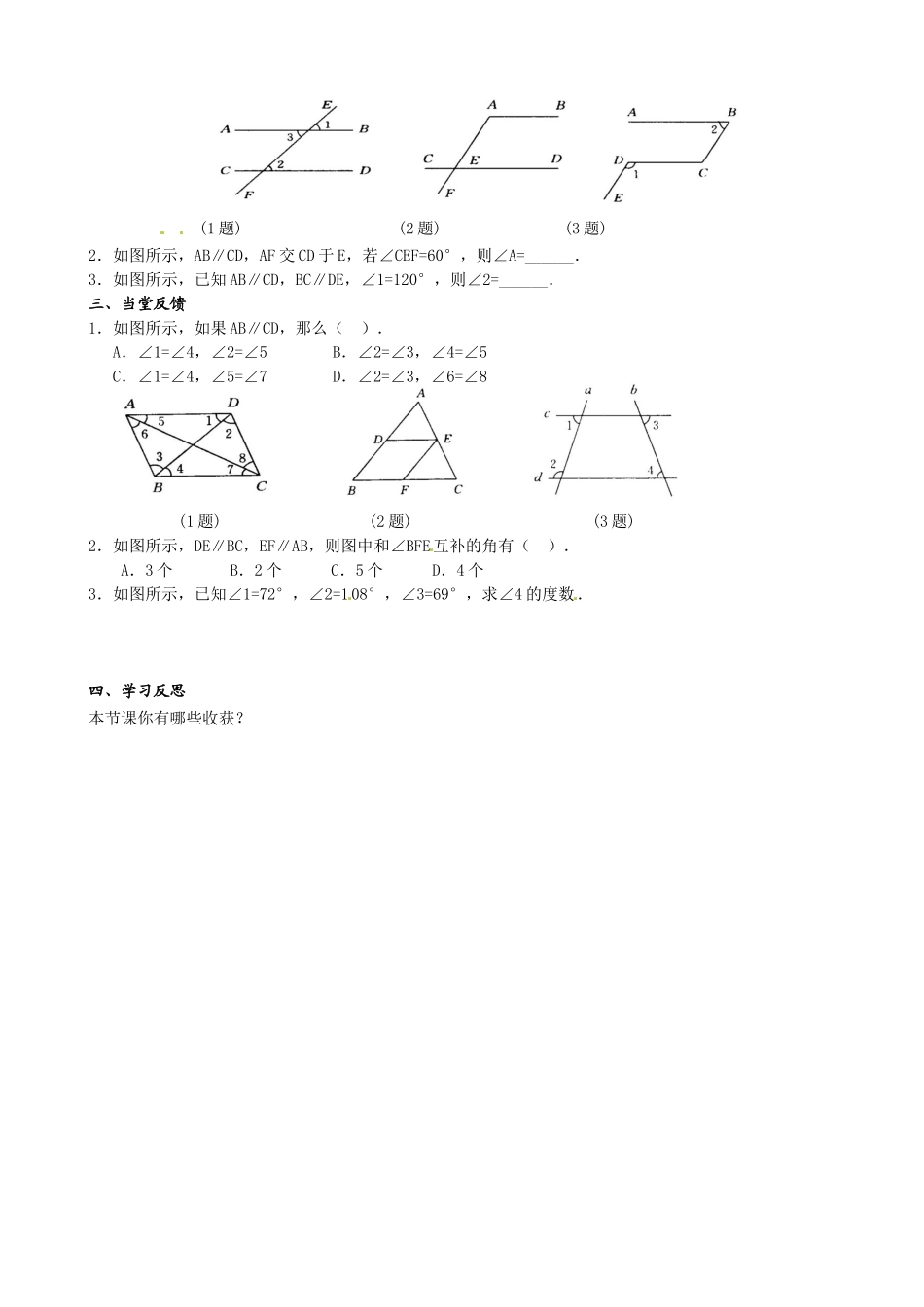
C12345BADEDCBA1A2A1B2B3B4B5B1C2C3C5C4C人教版七年级数学下册5.3.1平行线的性质【学习目标】1使学生掌握平行线的三个性质,并能应用它们进行简单的推理论证;2使学生经过对比后,理解平行线的性质和判定的区别和联系.【学习重点】平行线的三个性质及其应用.【学习难点】正确理解性质与判定的区别和联系,并正确运用它们去推理证明.【学习过程】一、学前准备二、探索思考探索一:请同学们仔细阅读课本P19页,完成课本上的探究.根据探究内容,我们可以得到平行线的性质,如图,将下列空白补充完整(填1种就可以)性质1(性质公理)几何语言表述为:∵AB∥CD∴∠___=∠___由性质1,结合对顶角的性质,我们可以得到:性质2(性质定理)几何语言表述为:∵AB∥CD∴∠___=∠___由性质1,结合邻补角的性质,我们可以得到:性质3(性质定理)几何语言表述为:∵AB∥CD∴∠___+∠___=练习一:1.根据右图将下列几何语言补充完整(1)∵AD∥(已知)∴∠A+∠ABC=180°()(2)∵AB∥(已知)∴∠4=∠()∠ABC=∠()2.如右图所示,BE平分∠ABC,DE∥BC,图中相等的角共有()A.3对B.4对C.5对D.6对3、如图,AB∥CD,∠1=45°,∠D=∠C,求∠D、∠C、∠B的度数.探索二:用三角尺和直尺画平行线,做成一张5×5个格子的方格纸.观察做出的方格纸的一部分(如图),线段B1C1、B2C2、…、B5C5都与两条平行的横线A1B5和A2C5垂直吗?它们的长度相等吗?像这样,同时垂直于两条平行直线,并且夹在这两条平行线间的线段的长度相等,叫做这两条平行线间的距离,即平行线间的距离处处相等.练习二:1.如图所示,已知直线AB∥CD,且被直线EF所截,若∠1=50°,则∠2=____,∠3=______.1ABCD83625147FEDCBA(1题)(2题)(3题)2.如图所示,AB∥CD,AF交CD于E,若∠CEF=60°,则∠A=______.3.如图所示,已知AB∥CD,BC∥DE,∠1=120°,则∠2=______.三、当堂反馈1.如图所示,如果AB∥CD,那么().A.∠1=∠4,∠2=∠5B.∠2=∠3,∠4=∠5C.∠1=∠4,∠5=∠7D.∠2=∠3,∠6=∠8(1题)(2题)(3题)2.如图所示,DE∥BC,EF∥AB,则图中和∠BFE互补的角有().A.3个B.2个C.5个D.4个3.如图所示,已知∠1=72°,∠2=108°,∠3=69°,求∠4的度数.四、学习反思本节课你有哪些收获?