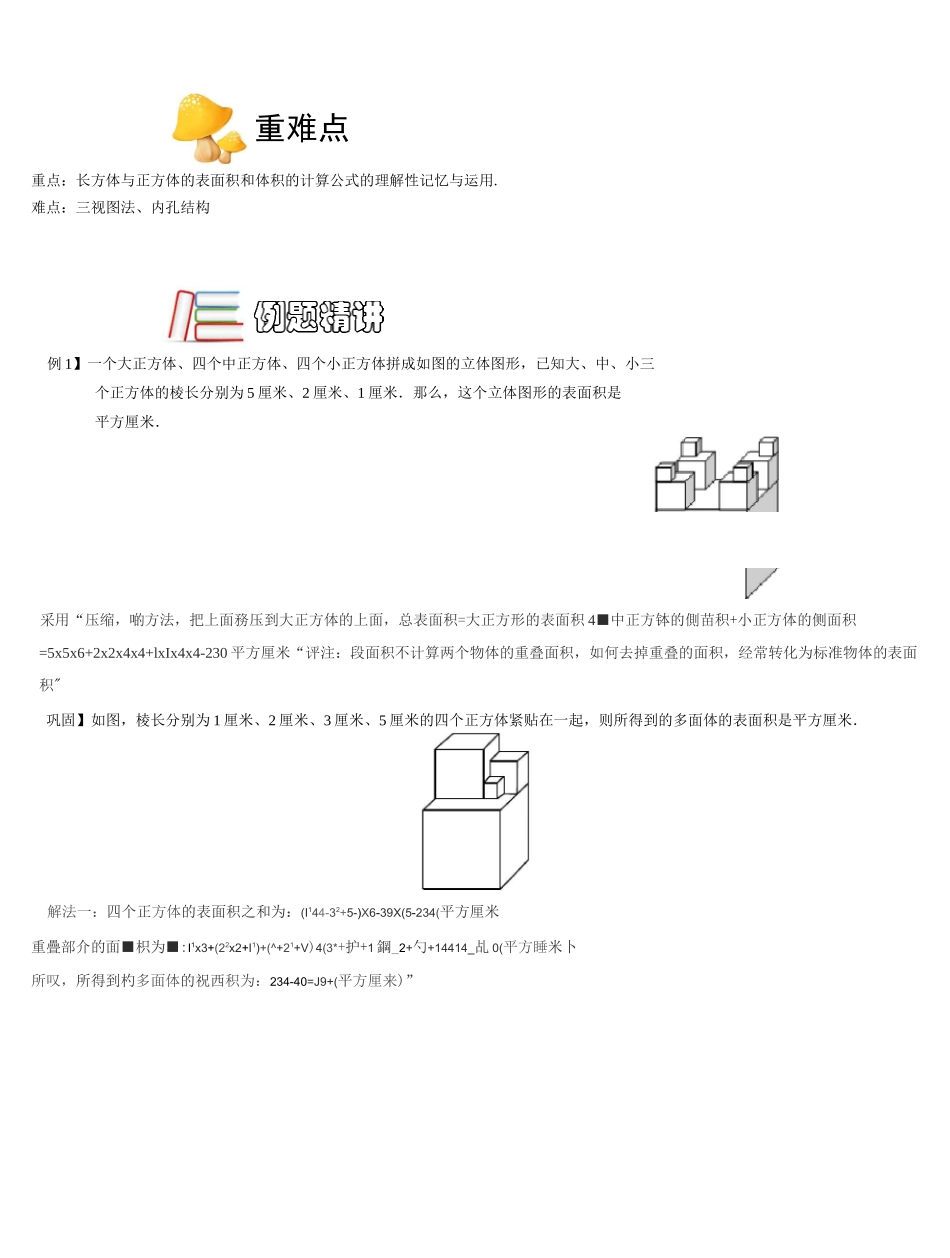
、立体图形的体积计算常用公式:立体图形示例表面积公式体积公式相关要素长方体/•j*S=2(ab+bc+ac)V=abhV=sh三要素:a、b、h二要素:s、ha.//正方体gS=6a2V=a3V=sh一要素:a二要素:s、h二、立体几何相关数学方法:接法:与平面几何中的方法类似,将不规则的图形体积化作规则图形的体积进行加减计算.1.视图法:主要适用于求正方体积木塔建图形的表面积计算.以及染色问题或计数问题,从上、前、左(下、后、右)这几个基本视角,分析图形的表面.2.片法:适用于求具有穿孔结构或内部结构的立体图形的体积计算,将立体图形沿某个方向切成多片,化立体为平面.舊长方体和正方体的表面积和体积;花\知识框架重难点重点:长方体与正方体的表面积和体积的计算公式的理解性记忆与运用.难点:三视图法、内孔结构例1】一个大正方体、四个中正方体、四个小正方体拼成如图的立体图形,已知大、中、小三个正方体的棱长分别为5厘米、2厘米、1厘米.那么,这个立体图形的表面积是平方厘米.采用“压缩,啲方法,把上面務压到大正方体的上面,总表面积=大正方形的表面积4■中正方钵的側苗积+小正方体的侧面积=5x5x6+2x2x4x4+lxIx4x4-230平方厘米“评注:段面积不计算两个物体的重叠面积,如何去掉重叠的面积,经常转化为标准物体的表面积"巩固】如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是平方厘米.解法一:四个正方体的表面积之和为:(I144-32+5-)X6-39X(5-234(平方厘米重疊部介的面■枳为■:I1x3+(22x2+I1)+(^+21+V)4(3*+护+1鋼_2+勺+14414_乩0(平方睡米卜所叹,所得到杓多面体的祝西积为:234-40=J9+(平方厘来)”弊法二:三视图法.从前后裔观察到的询积>?52+32-P21-3S平方厘米从左左两个面观察到的曲祺为宁十罗一34平右厘米,从二下能观祭到的曲积^52=25平方厘米.衷面积为I:豁十34十詰)聖_194(于方厘米],【例2】两个完全相同的长方体的长、宽、高分别为5厘米、4厘米、3厘米,把它们拼在一起可组成一个新长方体,在这些长方体中,表面积最小的是平方厘米。由于拼在一起可组成一个新辰方体:所以拼接的两个衙是完全相同的两个面,拼接成的长方体的面积,即等于原来的两金长方体的面积之和减去拼接在一起的两个面的面积,所说,在拼成的悅方体中:表面积最小的为拼接的两个面的面积鼠尢的情况,而原来的悅方体中:ftA_的面为弘4这个面,所叹,在拼成的这些长方体中,表面积最小的对:(5x4+4x3+3x5^4-5x4x2-18^-40-148〔平方厘米)“Id.【巩固】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?II:截去一个小正方体,表面积不变,只有在截去的小正方体的曲梱重合时,表面积才会诚少,所以要使朮块剩下部分的表面积辱可能小,应该在同一条樓的两端各裁去祓辰7与呂的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少義多.剩下部分的表面积鼠小是:15x15x6-7x7x2=1252+想想为彳十么15x15x6-7x7-KxH?例3】有一塔形几何体由若干个正方体构成,构成方式如下图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是./271抚几何体不论有多少层,其上、下表角积是囲定不变的,为2心+“工"它的每个側面的面积座该超i±(S9-S)-^4=7.75,最底层的正方体的单个侧面面积为2^2=4,往上依次为L匚丄,丄,24前五层正方体的单■金侧T©面积和■为4+2+1+-+-=7.75,24所汉妻想超i±7.75,至少应该是6个”【巩固】有n个同样大小的正方体,将它们堆成一个长方体,这个长方体的底面就是原正方体的底面.如果这个长方体的表面积是3096平方厘米,当从这个长方体的顶部拿去一个正方体后,新的长方体的表面积比原长方体的表面积减少144平方厘米,那么n为多少?由于堆成的悅方体的底面就是原来正方体的底面,说明这个枚方休是由这些正方休一字排开组成的,从这个悅方体的顶部拿去一个正方体,减少的面积相当于侧询的四个正方形的曲积,所以正...