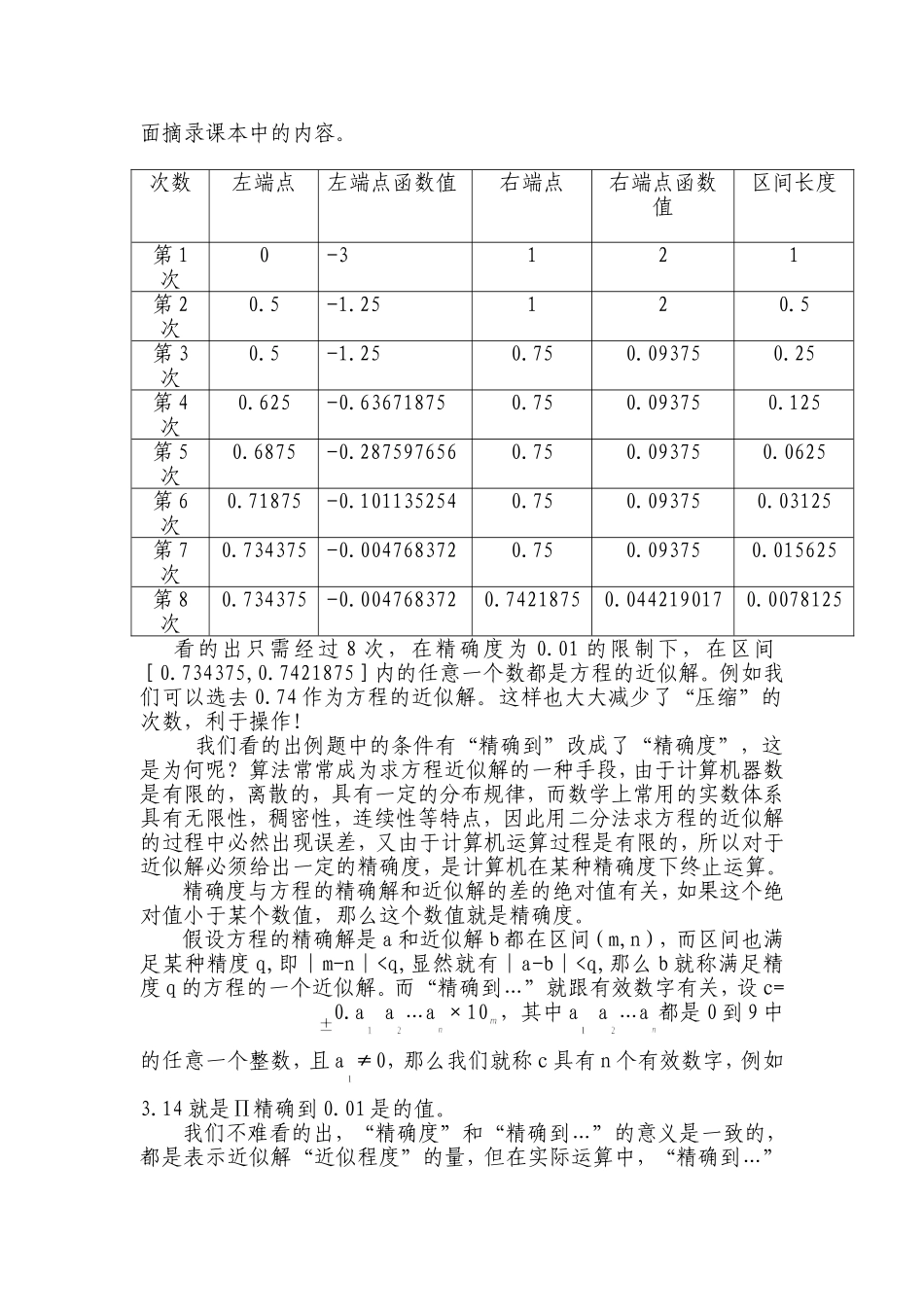
对新课标中用“用二分法求方程的近似解”的修正见解类型:论文作者姓名:鄢争艳职称:中学一级单位:江西省丰城拖船中学手机:13576159674地址:江西省丰城拖船中学邮编:331122对新课标中用“用二分法求方程的近似解”的修正见解在北师大版《必修一》中“用二分法求方程的近似解”一节中2009年版和2010年版对同一个例题作出了两个不同的安排,或者说是作了一些改进,这其中有何用意呢?下面本人结合自己的教学经历作了一些分析,以供大家参考。2009年版的例题:求方程2x+3x-3=0的一个实数解,精确到0.01解:因为f(0)=-3<0,f(1)=2>0.所以方程在[0,1]内有解。下面摘录课本中的内容。次数左端点左端点函数值右端点右端点函数值第1次0-312第2次0.5-1.2512第3次0.5-1.250.750.09375第4次0.625-0.636718750.750.09375第5次0.6875-0.2875976560.750.09375第6次0.71875-0.1011352540.750.09375第7次0.734375-0.0047683720.750.09375第8次0.734375-0.0047683720.74218750.044219017第9次0.734375-0.0047683720.738281250.019657731第10次0.734375-0.0047683720.7363281250.007427827第11次0.734375-0.0047683720.7353515630.00132552第12次0.734863281-0.0017224770.7353515630.00132552第13次0.735107422-0.0001987420.7353515630.00132552到第13次时在区间[0.735107422,0.735351563]中任取一个数精确到0.01的值都是0.75,所以方程的一个实数解为0.735.通过上述计算不难发现,在精确到0.01下方程的一个近似解为0.735,而0.735落在“压缩”所得的区间之外,能否有效地,深刻地刻画“二分法的”逐步逼近思想?另一方面,仅仅用“压缩”所得的小区间的两个端点值的统一近似值作为方程的近似解,是否科学,合理地呈现“二分法”的极限思想?“二分法”中心思想是两边“逐步夹逼”,渗透了极限的思想,核心问题是“逐步逼近”上述解法方程的近似解0.735游离在“夹逼”所得的小区间[0.735107422,0.735351563]之外,近似解变成了尴尬,无奈区间的局外值,给人感觉越逼近,反而离得越远,进行这么多次的夹逼是多此一举,有“雾里看花,虚化,冷化”之嫌,难于旗帜鲜明地彰显“二分法”的逐步逼近思想和极限思想!用“二分法”求方程的近似解,如果所得的近似解落在逐步夹逼的小区间(m,n)内,无论是从表象上看,还是从深层次的内涵,实质上看,是不是更合理,更具说服力,更有效的体现了“二分法”的“逐步逼近”思想和极限思想呢;另一方面,“夹逼”所得的小区间(m,n)的两个端点的数值m,n按照精确度得要求,区间左端点值m向右“逼近”,区间右端点值n向左“逼近”,即(m→p←n),这样的近似值p作为方程的近似解是不是更具“逼近”的味道呢!是不是更科学,更深刻地刻画了“二分法”的思想精髓呢!按照这样的修正新课标2010年版的这个例题是这样叙述的:求方程2x+3x-3=0的近似解,精度为0.01解:因为f(0)=-3<0,f(1)=2>0.所以方程在[0,1]内有解。下面摘录课本中的内容。次数左端点左端点函数值右端点右端点函数值区间长度第1次0-3121第2次0.5-1.25120.5第3次0.5-1.250.750.093750.25第4次0.625-0.636718750.750.093750.125第5次0.6875-0.2875976560.750.093750.0625第6次0.71875-0.1011352540.750.093750.03125第7次0.734375-0.0047683720.750.093750.015625第8次0.734375-0.0047683720.74218750.0442190170.0078125看的出只需经过8次,在精确度为0.01的限制下,在区间[0.734375,0.7421875]内的任意一个数都是方程的近似解。例如我们可以选去0.74作为方程的近似解。这样也大大减少了“压缩”的次数,利于操作!我们看的出例题中的条件有“精确到”改成了“精确度”,这是为何呢?算法常常成为求方程近似解的一种手段,由于计算机器数是有限的,离散的,具有一定的分布规律,而数学上常用的实数体系具有无限性,稠密性,连续性等特点,因此用二分法求方程的近似解的过程中必然出现误差,又由于计算机运算过程是有限的,所以对于近似解必须给出一定的精确度,是计算机在某种精确度下终止运算。精确度与方程的精确解和近似解的差的绝对值有关,如果这个绝对值小于某个数值,那么这个数值就...