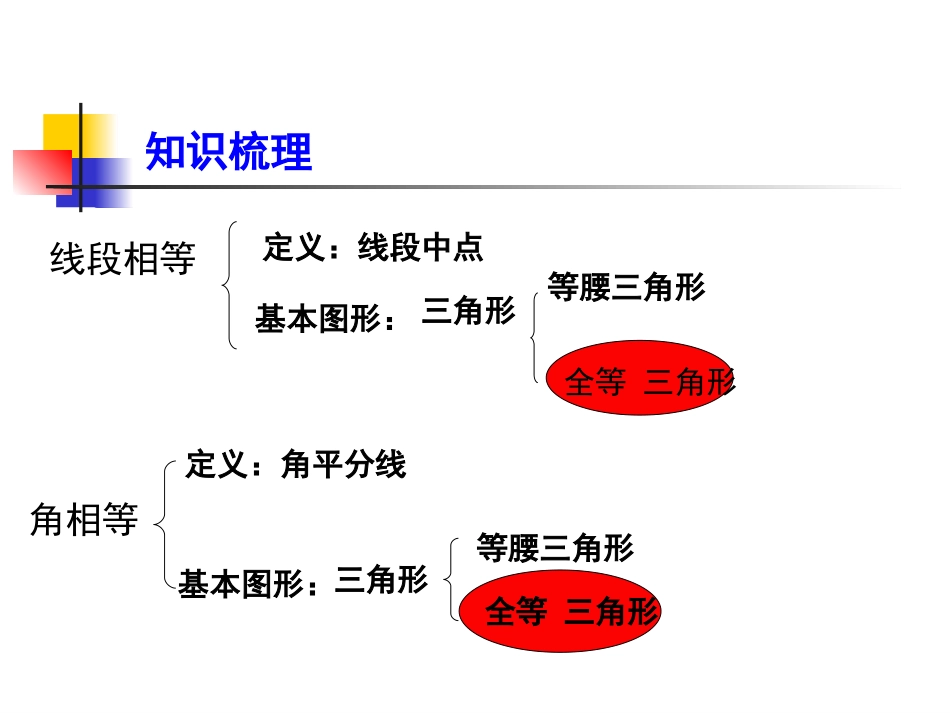
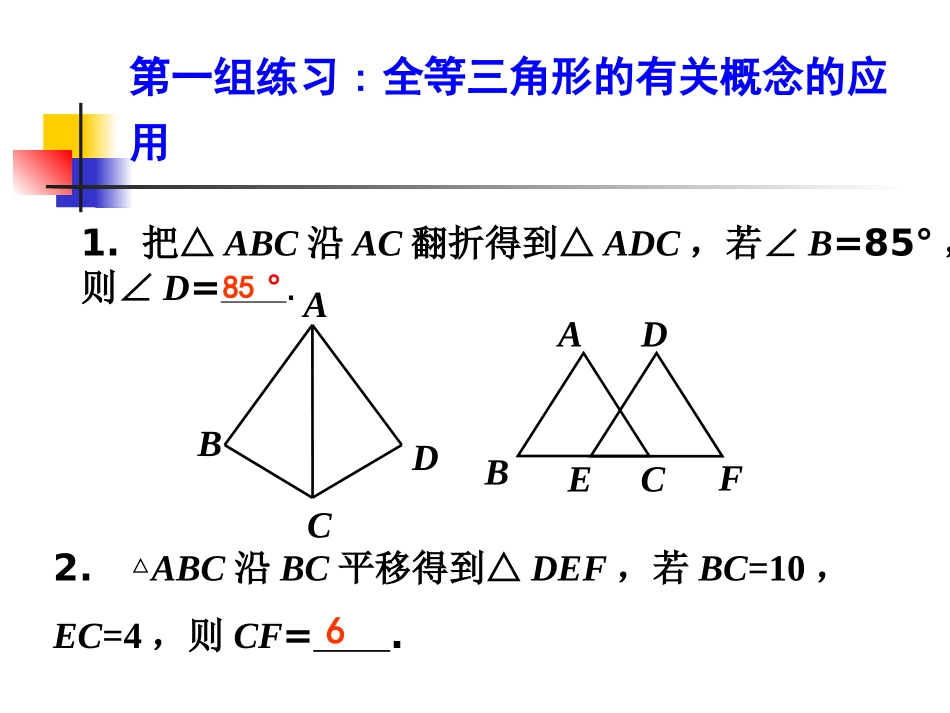
第十二章全等三角形北京市安慧北里中学张秀国章末小结(章末小结(BB案)案)线段相等定义:线段中点基本图形:三角形等腰三角形全等三角形角相等定义:角平分线三角形基本图形:等腰三角形全等三角形知识梳理第一组练习:全等三角形的有关概念的应用1.把△ABC沿AC翻折得到△ADC,若∠B=85°,则∠D=.DBACFEDCBA2.△ABC沿BC平移得到△DEF,若BC=10,EC=4,则CF=.85°6第一组练习:全等三角形的有关概念的应用3.把△ABC绕点A旋转至△ADE的位置,∠C=∠E,若∠BAC=90°,∠DAC=55°,则∠CAE=.ABDCE35°第二组练习:全等三角形性质的应用1.△ABC≌△BAD,A和B、C和D是对应点,如果BD=5cm,AD=4cm,AB=6cm,那么BC的长是()A.6cmB.5cmC.4cmD.无法确定2.如图,△ACB≌△A′CB′,A和A′,B和B′是对应点,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°CBODCBABAB'CA'第二组练习:全等三角形性质应用3.如图,OA=OB,OC=OD,∠O=65°,∠D=35°,则∠AEC等于()A.60°B.50°C.45°D.30°CACEDBO第二组练习:全等三角形性质应用(选做题)4.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,把Rt△ABC绕点A逆时针旋转60°,得到△ADE,问△ABD的形状;旋转90°呢?GSP选做题答案:等边三角形;等腰直角三角形EDABC第三组练习:三角形全等的判定1.请填出使两个三角形全等的条件,并把条件标注在图形上.在△ABC和△A′B′C′中,_____=_____,_____=_____,_____=_____,∴△ABC≌△A′B′C′.CBAA'B'C'感悟提升全等三角形对应边相等对应角相等平移、翻折、旋转找条件(至少有一组对应边相等)第三组练习:三角形全等的判定2.工人师傅常用角尺平分一个任意角.作法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C作射线OC.由此作法得△MOC≌△NOC的依据是()A.AASB.SASC.ASAD.SSSB第三组练习:三角形全等的判定3.如图,AC、BD相交于O,OA=OC,请你添加一个条件,使△AOB≌△COD,并说明理由.△AOB≌△CODSASOA=OC∠DOC=∠AOBOD=OB还有其他添法吗?∠C=∠A(ASA)或∠D=∠B(AAS)DCOBA第四组练习:三角形全等的应用1.如图AB=DC,AC=BD.求证:∠A=∠D.DCOBA证明:在△ABC和△DCB中,AB=DC,AC=BD,BC=CB(公共边),∴△ABC≌△DCB,∴∠A=∠D.由图可得公共边BC=BC第四组练习:三角形全等的应用2.如图OD=OC,OA=OB.求证:AD=BC.OEABDC证明:在△ODA和△OCB中,OD=OC,∠O=∠O(公共角),OA=OB,∴△ODA≌△OCB,∴AD=BC.由图可得公共角∠o=∠o第四组练习:三角形全等的应用3.如图,AD与BE相交于点C,AC=DC,BC=EC.求证:AB∥ED.DCAEB证明:在△ACB和△DCE中,AC=DC,∠ACB=∠DCE(对顶角),BC=EC,∴△ACB≌△DCE,∴∠A=∠D,∴AB∥ED.由图可得对顶角∠ACB=∠DCE感悟提升对应角相等图形语言(公共边公共角对顶角)全等三角形对应边相等找条件(至少有一组对应边相等)第四组练习:三角形全等的应用4.AC⊥EF于点C,AH⊥FD于点B,∠E=90°,AC=FE.求证:AH=FD.DFABCEGH证明: AC⊥EF,AH⊥FD,∴∠ABG=∠FCG=90°. ∠FGC=∠AGB,∴∠A=∠F. AC⊥EF,∴∠ACH=90°.在△ACH和△FED中,∠A=∠F,AC=FE,∠A=∠F,∴△ACH≌△FED,AH=FD.FEABDC第四组练习:三角形全等的应用5.在△ABC中,AD平分∠BAC,BD=CD,DE⊥AB于点E,DF⊥AC于点F.求证:BE=CF.证明: AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF. DE⊥AB,DF⊥AC,∴△BED和△BED是直角三角形.在Rt△BED和Rt△CFD中,BD=CD,DE=DF,∴Rt△BED≌Rt△CFD.∴BE=CF.感悟提升找条件(至少有一组对应边相等)边相等(等角对等边,角平分线的性质,线段中点)角相等(垂直,平行,角平分线,同(等)角的余(补)角相等)全等三角形平移、翻折、旋转对应边相等对应角相等图形语言(公共边,公共角,对顶角)第五组练习:综合运用1.△ABC是等腰三角形,D、E分别是腰AB及AC延长线上的一点,且BD=CE,连接DE交底BC于点G.求证:GD=GE.解题思路:过点D作DM∥CE,构造等腰△DMB,再得出△DMG≌△ECG,即得出结论.M思考:GD和GE不在两个全等三角形中,如何证明相等呢?GEDCBA感悟提升找条...