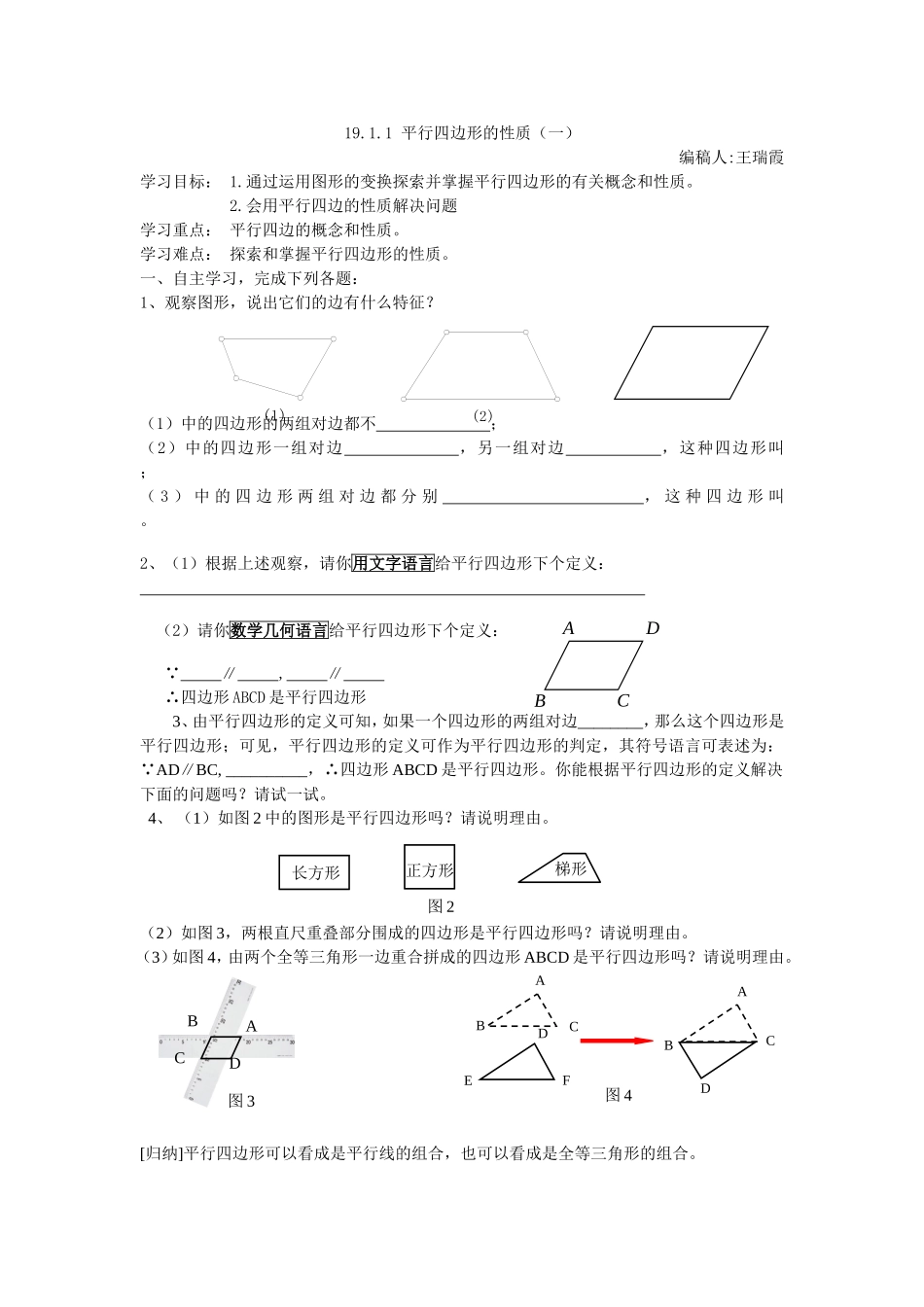
19.1.1平行四边形的性质(一)编稿人:王瑞霞学习目标:1.通过运用图形的变换探索并掌握平行四边形的有关概念和性质。2.会用平行四边的性质解决问题学习重点:平行四边的概念和性质。学习难点:探索和掌握平行四边形的性质。一、自主学习,完成下列各题:1、观察图形,说出它们的边有什么特征?(1)中的四边形的两组对边都不;(2)中的四边形一组对边,另一组对边,这种四边形叫;(3)中的四边形两组对边都分别,这种四边形叫。2、(1)根据上述观察,请你用文字语言给平行四边形下个定义:(2)请你数学几何语言给平行四边形下个定义:∵∥,∥∴四边形ABCD是平行四边形3、由平行四边形的定义可知,如果一个四边形的两组对边________,那么这个四边形是平行四边形;可见,平行四边形的定义可作为平行四边形的判定,其符号语言可表述为:∵AD∥BC,__________,∴四边形ABCD是平行四边形。你能根据平行四边形的定义解决下面的问题吗?请试一试。4、(1)如图2中的图形是平行四边形吗?请说明理由。(2)如图3,两根直尺重叠部分围成的四边形是平行四边形吗?请说明理由。(3)如图4,由两个全等三角形一边重合拼成的四边形ABCD是平行四边形吗?请说明理由。[归纳]平行四边形可以看成是平行线的组合,也可以看成是全等三角形的组合。(2)(1)ABDC正方形梯形长方形图2ABCDABCEDFABCD图3图4(二)探索平行四边形的性质平行四边形是四边形其内角和为3600,有两条对角线。由平行四边形的定义可知,平行四边形具有两组对边分别平行这一性质,(即∵四边形∵四边形ABCDABCD是平行四边形是平行四边形∴AB∥CDAB∥CD,,AD∥BCAD∥BC)。)。根据对边平行,我们又可得到平行四边形邻角互补的性质,(∠A+∠B=1800,∠B+∠C=1800)那么平行四边形还有其它的性质吗?让我们动手去探索发现吧。1、量一量:用直尺、量角器测量如图ABCD的边、角。AB=____;DC=____;AD=____;BC=____;∠A=____;∠C=____;∠B=____;∠D=____;2、猜一猜:仔细分析上面的测量结果,你能发现平行四边形的对边与对角有什么数量关系?猜想:。。3、证一证:猜想不一定正确,我们很难通过测量所有平行四边形来验证猜想,因而,证明:已知:如图,在ABCD中求证:AB=CD,AD=BC,∠A=∠C,∠B=∠D4、理一理:请用图形、文字、符号三种语言整理平行四边形的性质。文字语言:平行四边形的对边_____________、对角_________、邻角________。符号语言:∵四边形ABCD是平行四边形∴AD∥BC,_________(对边平行);AD=BC,__________(对边相等);∠A=∠C,_________(对角相等);∠A+∠B=180º…(邻角互补)。二、师生探究合作交流1.已知:口ABCD中,∠A=40°,你能求出其他各角的度数吗?说说你的理由。2.如图,已知:口ABCD中,周长等于24,AB=8,求其余三条边的长.ABCD图形ABCDABDCABDC3.在口ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=4,AF=6.口ABCD周长为40。求口ABCD的面积。三、学习体会1.本节课你有哪些收获?你还有哪些疑惑?2.你认为老师上课过程中还有那些需要注意或改进的地方?3.预习时疑难解决了吗?四、巩固练习1、如图,在口ABCD中,EF∥BC,GH∥AB,EF、GH相交于O,图中有_____个平行四边形2、在口ABCD中,∠A:∠B=4:5,那么∠B=__________,∠C=_________3、在口ABCD中,若AB=a,BC=b,则口ABCD的周长为_______4、已知口ABCD的周长为28cm,且AB∶BC=3∶4,则BC=______5、在口ABCD中,已知∠A+∠C=260°,则∠A=____,∠B=___,∠C=____,∠D=____。6、一个平行四边形的一个外角是380,这个平行四边形的每个内角的度数分别是多少?7、如图若已知平行四边形ABCD的周长为30cm,BC-AB=3,求平行四边形的各边长。ADCBFEOCDAGBEHFABCD8.如图,在□ABCD中,若BE平分∠ABC,则ED=.五、应用与拓展1、在平行四边形ABCD中,的平分线交CD于点E,的平分线交AB于点F,试判断AF与CE是否相等,并说明理由。EABDC9cm5cmABDCEF