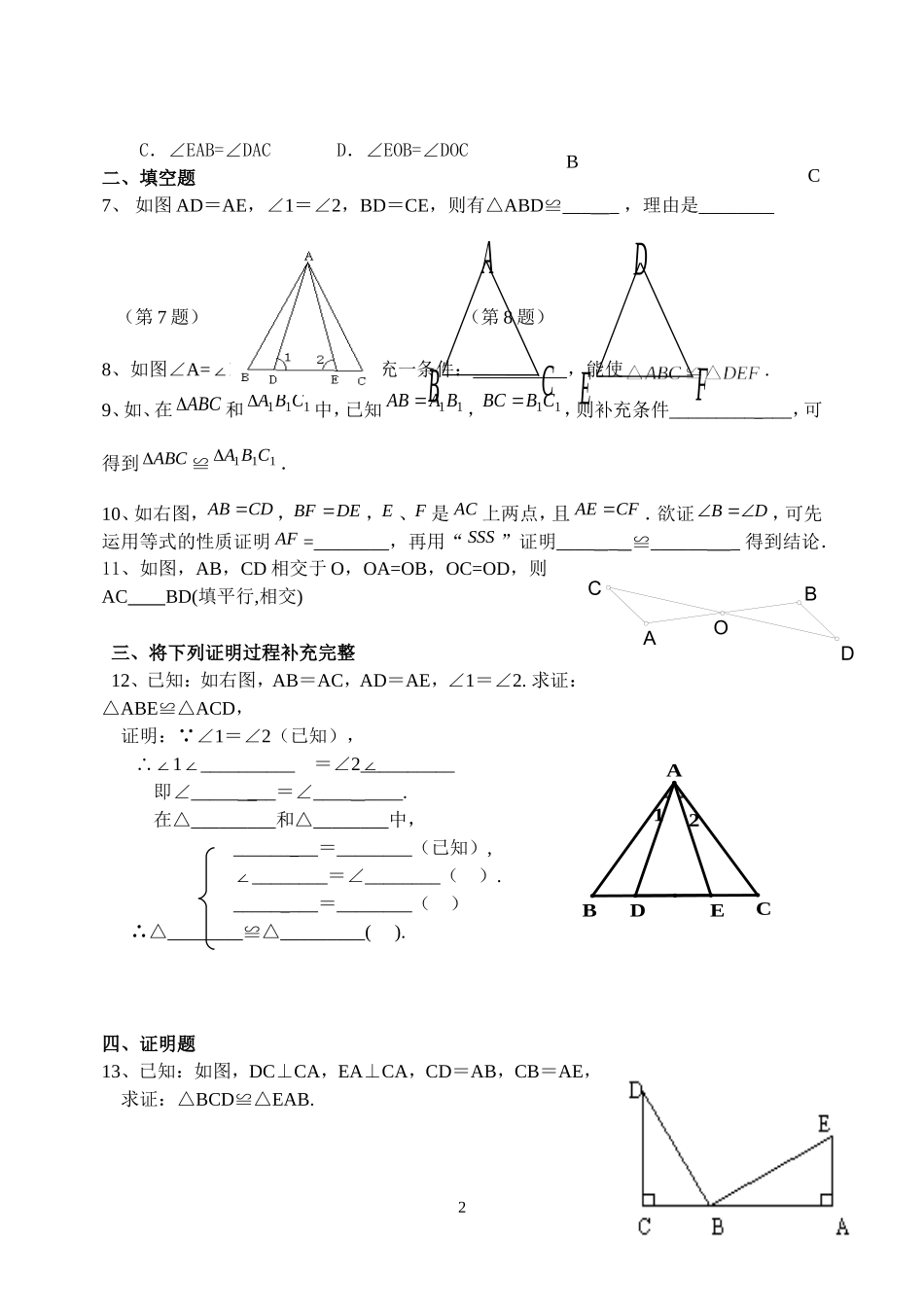
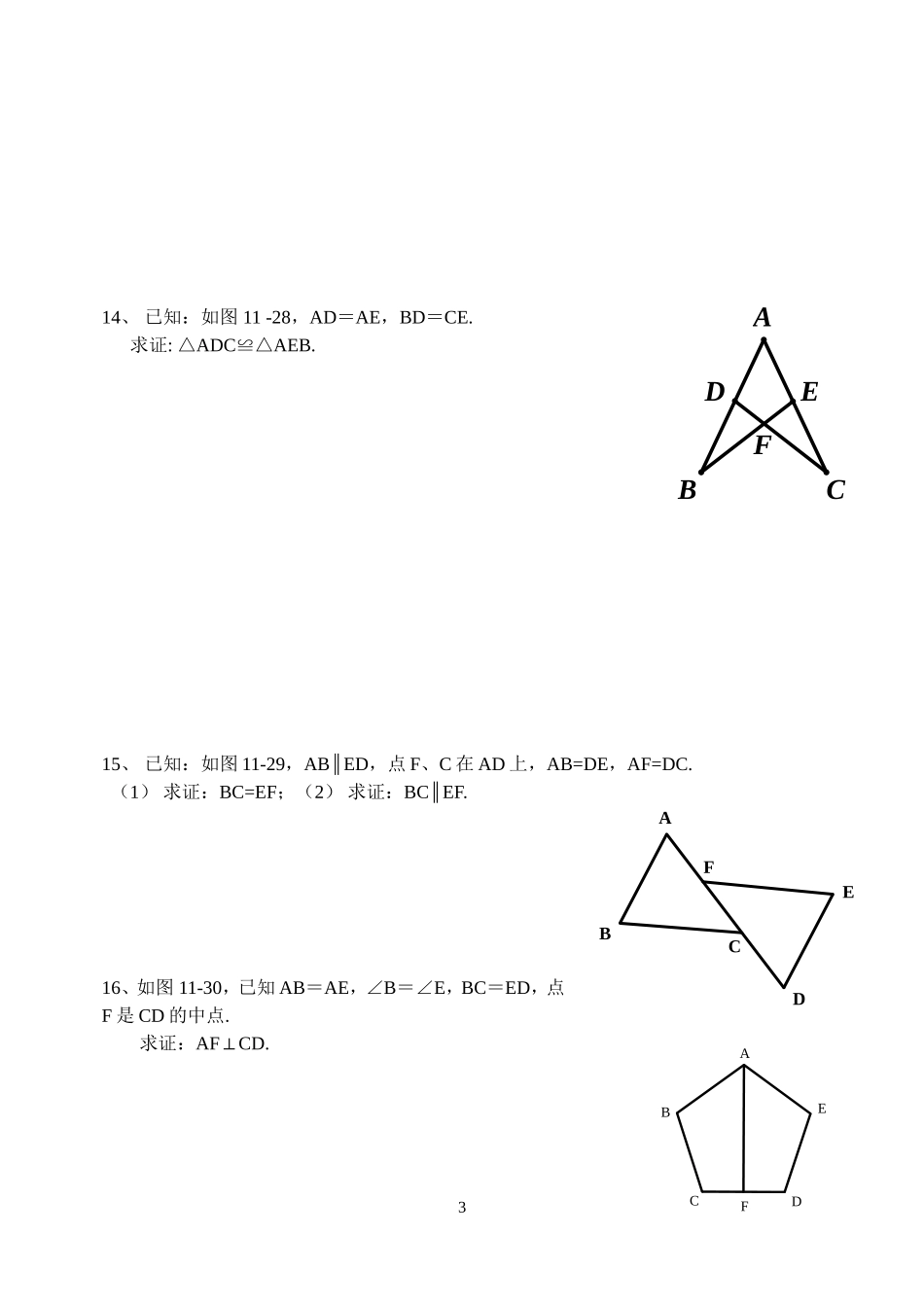
ODCBA全等三角形练习(SSS/SAS)一、选择题1、图中全等的三角形是()A.Ⅰ和ⅡB.Ⅰ和ⅢC.Ⅲ和ⅣD.Ⅱ和Ⅳ2、如右图,AB、CD相交于点O,AO=CO,若不再添加任何字母和辅助线,且只添加一个条件,使得△AODCOB≌△,则下列条件:①BO=COAD=CBOB=OD②③,那么可添加的有()A.B.C.D.①②③①②3、下列说法正确的是()A.全等三角形是指形状相同的两个三角形B.全等三角形的周长和面积分别相等C.全等三角形是指面积相等的两个三角形D.所有等边三角形都全等.4、如右图,在ABC中,ACAB,D为BC的中点,则下列结论中:①ABD≌ACD;②CB;③AD平分BAC;④BCAD,其中正确的个数为()A.1个B.2个C.3个D.4个5、下列条件中,可以确定△ABC和△A′B′C′全等的是()A.BC=BA,B′C′=B′A′,∠B=∠B′B.∠A=∠B′AC=A′B′AB=B′C′C.∠A=∠A′AB=B′C′AC=A′C′D.BC=B′C′AC=A′B′∠B=∠C′6、如图,根据“SAS”来判定△ABD≌△ACE,若已知AB=AC,AD=AE,则还需添条件()A.∠B=∠CB.∠D=∠E1Ⅲ9cm8cm30°Ⅱ8cm5cm30°Ⅰ8cm9cm30°Ⅳ8cm9cmDEAC.∠EAB=∠DACD.∠EOB=∠DOC二、填空题7、如图AD=AE,∠1=∠2,BD=CE,则有△ABD___≌_,理由是________(第7题)(第8题)8、如图∠A=D∠,AC=DF,则补充一条件:,能使.9、如、在ABC和111CBA中,已知11BAAB,11CBBC,则补充条件____________,可得到ABC≌111CBA.10、如右图,CDAB,DEBF,E、F是AC上两点,且CFAE.欲证DB,可先运用等式的性质证明AF=________,再用“SSS”证明_____≌_______得到结论.11、如图,AB,CD相交于O,OA=OB,OC=OD,则ACBD(填平行,相交)三、将下列证明过程补充完整12、已知:如右图,AB=AC,AD=AE,∠1=∠2.求证:△ABEACD≌△,证明:∵∠1=∠2(已知),1__________∴∠∠=∠2__________∠即∠________=∠________.在△_________和△________中,________=________(已知),________∠=∠________().________=________()_________________().∴△≌△四、证明题13、已知:如图,DC⊥CA,EA⊥CA,CD=AB,CB=AE,求证:△BCD≌△EAB.2ABCDEFCOADBBC21EDCBA14、已知:如图11-28,AD=AE,BD=CE.求证:ADCAEB.△≌△15、已知:如图11-29,ABED∥,点F、C在AD上,AB=DE,AF=DC.(1)求证:BC=EF;(2)求证:BCEF.∥16、如图11-30,已知AB=AE,∠B=∠E,BC=ED,点F是CD的中点.求证:AFCD.⊥3FABCDEFEDCBAFEDCBA17、如图,点B、E、C、F在同一直线上,CFBE,DEAB,DFAC.求证:DEGC18、如图,已知CDAB,BDAC,求证:DA.4