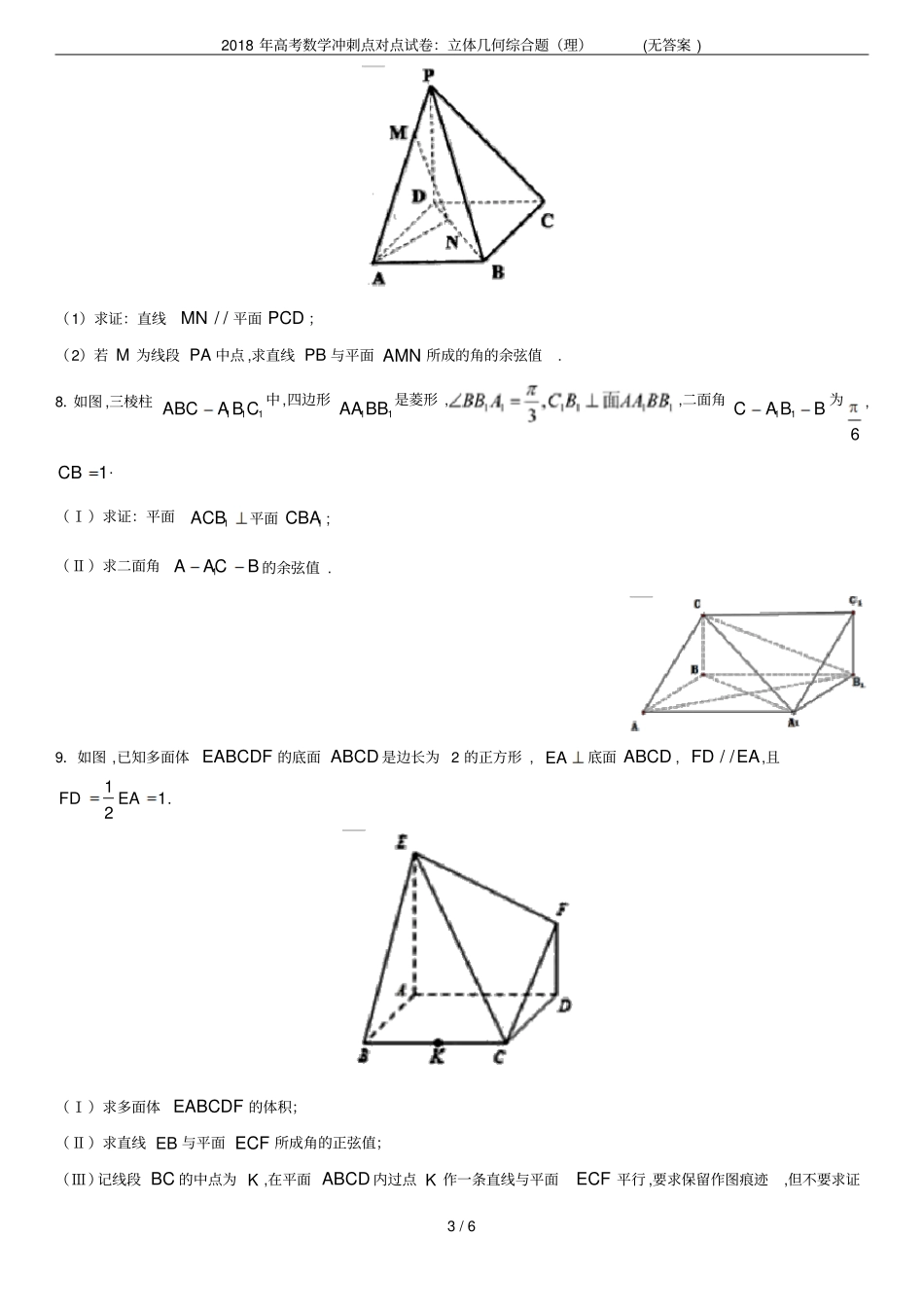
2018年高考数学冲刺点对点试卷:立体几何综合题(理)(无答案)1/6立体几何综合题(理)1.四棱柱1111ABCDABCD中,底面ABCD为正方形,1AA平面,ABCDM为棱1DD的中点,N为棱AD的中点,Q为棱1BB的中点.(1)证明:平面//MNQ平面1CBD;(2)若12AAAB,棱11AB上有一点P,且1110,1APAB,使得二面角PMNQ的余弦值为132163,求的值.2.如图,在五面体ABCDPN中,棱PA底面ABCD,2ABAPPN.底面ABCD是菱形,23BAD.(Ⅰ)求证:PNAB;(Ⅱ)求二面角BDNC的余弦值.3.如图四棱锥PABCD的底面ABCD为菱形,且60ABC,2ABPC,2PAPB.(Ⅰ)求证:平面PAB平面ABCD;(Ⅱ)二面角PACB的余弦值.4.如图,四棱锥PABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,ABBD7,2018年高考数学冲刺点对点试卷:立体几何综合题(理)(无答案)2/63PB.(Ⅰ)求证:平面PAD平面ABCD;(Ⅱ)设Q是棱PC上的点,当PA平面BDQ时,求二面角ABDQ的余弦值.5.如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BEAF,ABAF,122ABBEAF,3CBA,P为DF的中点.(Ⅰ)求证:PE∥平面ABCD;(Ⅱ)求二面角DEFA--的余弦值;(Ⅲ)设G为线段AD上一点,AGAD,若直线FG与平面ABEF所成角的正弦值为3926,求AG的长.6.在四棱锥PABCD中,底面ABCD为平行四边形,3AB,22AD,45ABC,P点在底面ABCD内的射影E在线段AB上,且2PE,2BEEA,F为AD的中点,M在线段CD上,且CMCD.(Ⅰ)当23时,证明:平面PFM平面PAB;(Ⅱ)当平面PAM与平面ABCD所成的二面角的正弦值为255时,求四棱锥PABCM的体积.7.如图,四棱锥PABCD底面为正方形,已知PD平面ABCD,PDAD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PMDN.2018年高考数学冲刺点对点试卷:立体几何综合题(理)(无答案)3/6(1)求证:直线//MN平面PCD;(2)若M为线段PA中点,求直线PB与平面AMN所成的角的余弦值.8.如图,三棱柱111ABCABC中,四边形11AABB是菱形,,二面角11CABB为6,1CB.(Ⅰ)求证:平面1ACB平面1CBA;(Ⅱ)求二面角1AACB的余弦值.9.如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA底面ABCD,//FDEA,且112FDEA.(Ⅰ)求多面体EABCDF的体积;(Ⅱ)求直线EB与平面ECF所成角的正弦值;(Ⅲ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证2018年高考数学冲刺点对点试卷:立体几何综合题(理)(无答案)4/6明.10.如图,四棱锥PABCD中,侧面PAD底面ABCD,//ADBC,ADDC,3ADDC,2BC,26PDPA,点F在棱PG上,且2FCFP,点E在棱AD上,且//PA平面BEF.(1)求证:PE平面ABCD;(2)求二面角PEBF的余弦值.11.如图所示的几何体中,ABC内接于圆O,且AB是圆O的直径,四边形DCBE为矩形,且DCAB.(Ⅰ)证明:ADBC;(Ⅱ)若4,2ABBC且二面角ABDC所成角的余弦值是55,试求该几何体ABCDE的体积.12.已知四棱锥PABCD的底面是平行四边形,EF,分别是ADPC,的中点,EFBD,22APABAD,0=60BAD.(Ⅰ)求证:BDAPB面;(Ⅱ)若ABPB,求二面角CBEF的余弦值.2018年高考数学冲刺点对点试卷:立体几何综合题(理)(无答案)5/613.如图1,在ABC中,9036CBCAC=,=,=,,DE分别是ACAB,上的点,且DEBC∥,2DE.将ADE沿DE折起到1ADE的位置,使1ACCD,如图2.(Ⅰ)M是1AD的中点,求CM与平面1ABE所成角的大小;(Ⅱ)求二面角1ABEC的正切值.14.如图,矩形CDEF所在平面与直角梯形ABCD所在平面垂直,其中//ABCD,11,22ABBCCD,BCCD,//MBFC,3MBFC.P、Q分别为BC、AE的中点.(1)求证://PQ平面MAB;(2)求二面角AECD的余弦值.15.如图所示,棱柱111ABCABC为正三棱柱,且1ACCC,其中点,FD分别为11,ACBB的中点.(1)求证://DF平面ABC;(2)求证:DF平面1ACC;(3)求平面1DCA与平面所成的锐二面角的余弦值2018年高考数学冲刺点对点试卷:立体几何综合题(理)(无答案)6/616.如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.(Ⅰ)求证:AF//平面BDH;学科!网(Ⅱ)求二面角A﹣FE﹣C的大小.