一元二次方程根与系数关系课件VIP免费

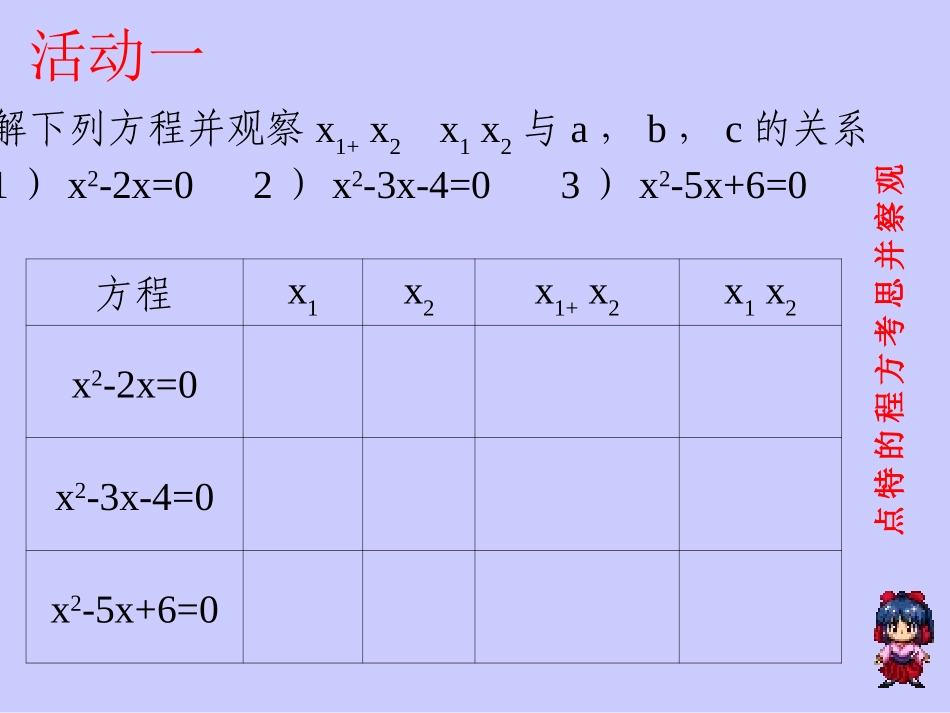
22.2.4一元二次方程根与系数的关系20(0)axbxca方程的求根公式是242bbacxa)(042acb2、解方程（1）x2-6x+8=0(2)2x2-3x+1=01、解下列方程并观察x1+x2x1x2与a，b，c的关系1）x2-2x=02）x2-3x-4=03）x2-5x+6=0方程x1x2x1+x2x1x2x2-2x=0x2-3x-4=0x2-5x+6=0观察并思考方程的特点活动一qxxpxxxxqpxx21212120,,则：，的两根为若方程特别地：为了研究问题的方便，我们把二次项系数为1的方程设为+px+q=0的形式，有上面表格得出以下结论：2x活动二解下列方程并观察x1+x2，x1x2与a，b，c的关系方程x1x2x1+x2x1x22x2+x-3=05x2-9x-2=02x2+3x-2=03x2+11x+6=0学生观察方程的特点并归纳总结x1+x2,x1x2与a，b，c的关系的系数有何关系？的值与方程你能看出的值试求出为的两根设方程2121212121200xxxxxxxxxxacbxax,.,,,)(对任意的一元二次方程，它的两根之和与两根之积与方程的系数都有这样的关系存在，就是baca12xx12xx此定理是法国数学家韦达首先发现的，也称为韦达定理一元二次方程根与系数的关系(韦达定理）acxxabxxxxacbxax212121200,,,)(则的两根为若方程qxxpxxxxqpxx21212120,,则：，的两根为若方程特别地：推论1你会证明吗？一元二次方程根与系数的关系(韦达定理）012121221xxxxxxxx）（）是方程（二次项系数为为根的一元二次以两个数,推论2acxxabxxxxacbxax212121200,,,)(则的两根为若方程例4、根据一元二次方程的根与系数的关系，求下列方程的X1，X2的和与积(1)x2-6x-15=0(2)3x2+7x-9=0(3)5x-1=4x2注意的三个问题：1、化成一般式；2、二次项系数化1；3、不要漏掉-的负号。已知方程5x2+kx-6=0的一个根是2，求另一个根及k值。1、如果-1是方程2X2－X+m=0的一个根，则另一个根是___，m=____。2、设X1、X2是方程X2－4X+1=0的两个根，则X1+X2=___,X1X2=____，X12+X22=(X1+X2)2-___=___(X1-X2)2=(___)2-4X1X2=___3、判断正误：以2和-3为根的方程是X2－X-6=0（）4、已知两个数的和是1，积是-2，则这两个数是_____。X1+X22X1X2-3411412×2和-1基础练习（还有其他解法吗？）231、求下列方程的两根之和与两根之积.1）x2-3x+1=02）2x2-9x+5=03）4x2-7x+1=04）2x2+3x=05）6x2-1=06）3x2-2x=-27）3x2=12、已知方程3x2-19x-+m=0的一根是1，求另一根及m的值。基础练习解：设方程的两个根是x1x2那么x1+x2=-—x1.x2=-—.33222211例例22不解方程，求方程不解方程，求方程22x2+3x-1=0的两个根的（1）（2）（1）∵（x1+x2）2=x12+2x1.x2+x22∴x12+x22=（x1+x2）2-2x1.x2=（-—）2-2（-—）=—332222111313441（2）—+—=————=———=3x111x1.x2x1+x2x2112232221xx21x1x1月考重点题已知方程的两个实数根是,(1)求k的取值范围（2）是否存在K的值使得若存在求出K的值解：由根与系数的关系得X1+X2=-k，X1×X2=k+2又X12+X22=4即(X1+X2)2-2X1X2=4K2-2(k+2）=4K2-2k-8=0∵△=K2-4k-8当k=4时，△＜0当k=-2时，△＞0∴k=-2解得：k=4或k=－2022kkxx2,1xx4xx2221练习：P42练习小结你有什么收获？acxxabxxxxacbxax212121200,,,)(则的两根为若方程qxxpxxxxqpxx21212120,,则：，的两根为若方程特别地：推论1012121221xxxxxxxx）（）是方程（二次项系数为为根的一元二次以两个数,推论21、课本43页习题22.2第7题。2、思考题m取何值时方程x2+mx+m-1=0（1）两根之和为1（2）两根之积为-1（3）两根互为倒数（4）两根互为相反数作业