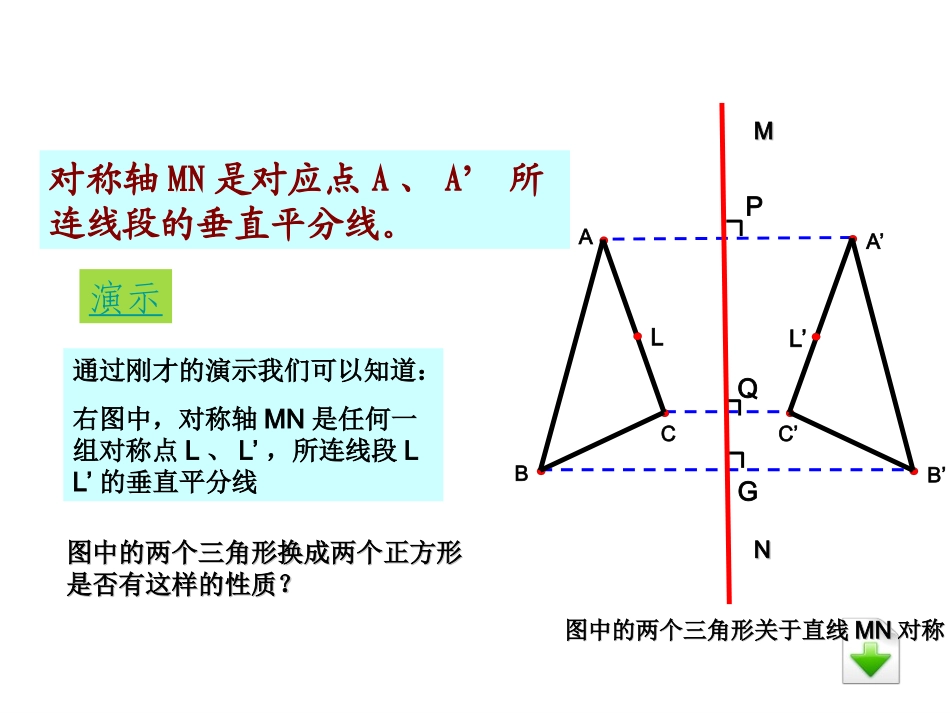
MN⊥AA’于PAP=A’P1、图中的对称点有哪些?2、点A和A’的连线与直线MN有什么样的关系?图中的两个三角形关于直线图中的两个三角形关于直线MNMN对称对称直线直线MNMN垂直且平分线段垂直且平分线段AAA’A’定义:经过线段的中点并且垂直于这条线段,就叫这条线段的垂直平分线,也叫中垂线。MMNNABCA’C’B’PQG图中的两个三角形关于直线图中的两个三角形关于直线MNMN对称对称MMNNABCA’C’B’PQG对称轴MN是对应点A、A’所连线段的垂直平分线。LL’图中的两个三角形换成两个正方形图中的两个三角形换成两个正方形是否有这样的性质?是否有这样的性质?通过刚才的演示我们可以知道:右图中,对称轴MN是任何一组对称点L、L’,所连线段LL’的垂直平分线演示通过前面的研究我们就可以得到图形轴对称的性质:如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线。类似地,轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线.演示前面的两个性质可以简单的概括为:前面的两个性质可以简单的概括为:对应点的连线被对称轴垂直平分对应点的连线被对称轴垂直平分。。如果我们感觉一个图形是轴对称图形,我们如何验证呢?不折叠图形你能准确地得出它的对称轴吗?思考AA’作出一对对称点的垂直平分线,就得到它的对称轴。现给出对称图形的一半你能否做出另外的部分?B'C'A'FEDACB下面我们来探究线段垂直平分线的性质猜想:线段垂直平分线上的点与这条线段两个端点的距离相等.即AP1=BP1,AP2=BP2,…能用我们已有的知识来证明这个结论吗?P3ABlP2P1演示l是AB的垂直平分线,观察P1A和P1B,P2A和P2B,P3A和P3B之间的关系?求证:线段垂直平分线上得点到这条线段两端的距离相等BACPl同学们能不能根据这幅图用符号语言来描述这个命题并给予证明呢?转化成数学语言:已知:直线m是线段AB的垂直平分线,P为线段AB上的任意一点;求证:PA=PB.证明:利用判定两个三角形全等.∵m是AB的垂直平分线,P在m上∴PCAB,AO=BO⊥∴∠AOP=BOP=90∠°在△APO和△BPO中,∴△APOBPO(SAS)≌△∴PA=PB.PO=PO∠AOP=BOP∠AO=BO结论:线段垂直平分线上的点与这条线段结论:线段垂直平分线上的点与这条线段两个端点的距离相等.两个端点的距离相等.ABPlC11、因为、因为ADAD为为BCBC的中垂线,所以的中垂线,所以。。理由:理由:ABAB==ACAC线段垂直平分线上的点与这条线段垂直平分线上的点与这条线段两个端点的距离相等.线段两个端点的距离相等.BBCCAADD2、如图,NMNM是线段是线段ABAB的中垂线的中垂线,,下列说法正确的有下列说法正确的有::。。①①AB⊥MN,②AD=DBAB⊥MN,②AD=DB,③,③MN⊥ABMN⊥AB,,④④MD=DNMD=DN,⑤,⑤ABAB是是MNMN的垂直平分的垂直平分线线ABMND①②③①②③如图,若如图,若AC=12AC=12,,BC=7BC=7,,ABAB的垂直平分的垂直平分线交线交ABAB于于EE,交,交ACAC于于DD,求△,求△BCDBCD的周的周长。长。DCBEA解:∵∵EDED是线段是线段ABAB的垂直平分线的垂直平分线∴∴∵△∵△BCDBCD的周长的周长=BD+DC+BC=BD+DC+BC∴△∴△BCDBCD的周长的周长======BD=ADBD=ADAD+DC+BCAD+DC+BCAC+BCAC+BC12+7=1912+7=19习题1.如图,ADBC⊥,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?ADBEC证明:∵ADBCBD=DC⊥∴AD在线段BC的垂直平分线上∴AB=AC∵点C在AE的垂直平分线上∴AC=CE又AB=AC∴AB=AC=CE∵AB=AC=CE又BD=CD∴AB+BD=CE+CD=DE2、如下图△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,求BC的长。AEDBCCDOBPANM解:PAONONPA与关于对称为的中垂线(……)DA=DP()CB=CP同理可有:PCDPC+PD+CDPCDBC+AD+CDABAB15cmPCD周长=周长==又=周长为15cmPPAONBOMABMON已知:为内一点。与关于对称,P与关于对称。若长为15cm求:PCD的周长.4、如图,在Rt△ABC中,∠C=90,DE是AB的垂直平分线,连接AE,∠CAE:∠DAE=1:2,求∠B的度数。AEDBC总结•本节课我们学习了:1、垂直平分线2、图形轴对称的性质3、中垂线的性质36页习题12.1─3、4、9题