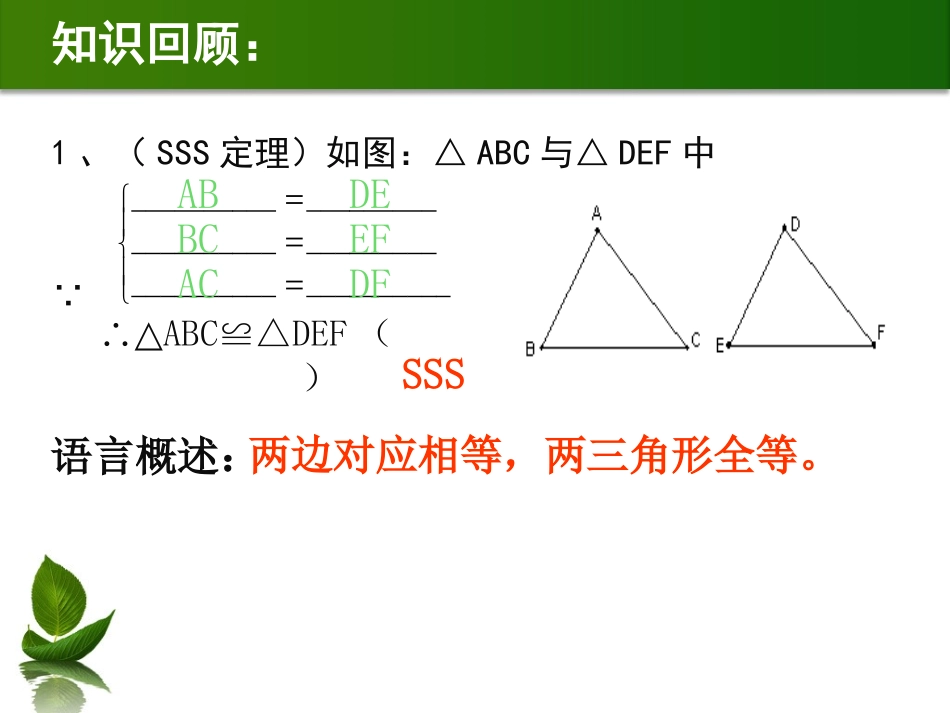
一.全等三角形:1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?2:全等三角形有哪些性质?能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。(1)全等三角形的对应边相等、对应角相等。(2)全等三角形的周长相等、面积相等。(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。知识回顾:1、(SSS定理)如图:△ABC与△DEF中 __________________________________________________________语言概述:EFBCDFACDEABSSS∴△ABC≌△DEF()两边对应相等,两三角形全等。2、(SAS定理)如图:△ABC与△DEF中 __________________________________________________________语言概述:∠BEFBCDEABSAS∴△ABC≌△DEF()两边及夹角对应相等,两三角形全等。∠E知识回顾:3、(ASA定理)如图:△ABC与△DEF中 __________________________________________________________语言概述:AB∠E∠B∠D∠AASA∴△ABC≌△DEF()三边及夹角对应相等,两三角形全等。DE知识回顾:4、(AAS定理)如图:△ABC与△DEF中 __________________________________________________________语言概述:∠BEFBC∠D∠AAAS∴△ABC≌△DEF()两角及其中一条对应相等,两三角形全等。∠E知识回顾:5、(HL定理)如图:Rt△ABC与Rt△DEF中,∠A=∠D=90° 语言概述:ABEFBCHL∴Rt△ABC≌Rt△DEF()斜边及一条直角边对应相等的两个直角三角形全等。DE知识回顾:一般三角形全等的条件:1.定义(重合)法;2.SSS;3.SAS;4.ASA;5.AAS.直角三角形全等特有的条件:HL.包括直角三角形不包括其它形状的三角形解题中常用的4种方法知识回顾:边边边:三边对应相等的两个三角形全等(可简写成“SSS”)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)知识回顾:证明两个三角形全等的基本思路:(1)已知两边----找第三边(SSS)找夹角(SAS)(2)已知一边一角---已知一边和它的邻角找是否有直角(HL)已知一边和它的对角找这边的另一个邻角(ASA)找这个角的另一个边(SAS)找这边的对角(AAS)找一角(AAS)已知角是直角,找一边(HL)(3)已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)方法指引:4:全等三角形的性质 △ABC≌△DEF∴AB=,AC=,BC=,∠A=,∠B=,∠C=;①全等三角形的对应边全等三角形的对应角②全等三角形的周长、面积。对应边上的对应、、分别相等。二.全等三角形的性质与判定定理的运用举例1、如图1,已知△ABE≌△DCE,AE=2cm,BE=1.5cm,∠A=25°∠B=48°;那么DE=cm,EC=cm,∠C=度;∠D=度;EBADC(第1小题)2、如图2,已知,∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“SAS”为依据,还须添加的一个条件为;(2)若以“ASA”为依据,还须添加的一个条件为;(3)若以“AAS”为依据,还须添加的一个条件为;FEDCBA(第2小题)4、如图4,平行四边形ABCD中,图中的全等三角形是;OCADB如图34、如图4,已知∠CAB=∠DBA,要使△ABC≌△BAD,只需增加的一个条件是;(只需填写一个你认为适合的条件)DCBA如图45、分别根据下列已知条件,再补充一个条件使得下图中的△ABD和△ACE全等;(1)AB=AC,∠A=∠A,;(2)AB=AC,∠B=∠C;(3)AD=AE,,DB=CE.如图5EDCBA6、如图,AC=BD,BC=AD,说明△ABC和△BAD全等的理由.证明:在△ABC与△BAD中, ∴△ABC≌△BAD()______________________________________________ABCD如图67、如图,CE=DE,EA=EB,CA=DB,求证:△ABC≌△BAD.证明 CE=DE,EA=EB∴=在△ABC和△BAD.中, ______________________________________________已证已知∴△ABC≌△BAD.()三.课...