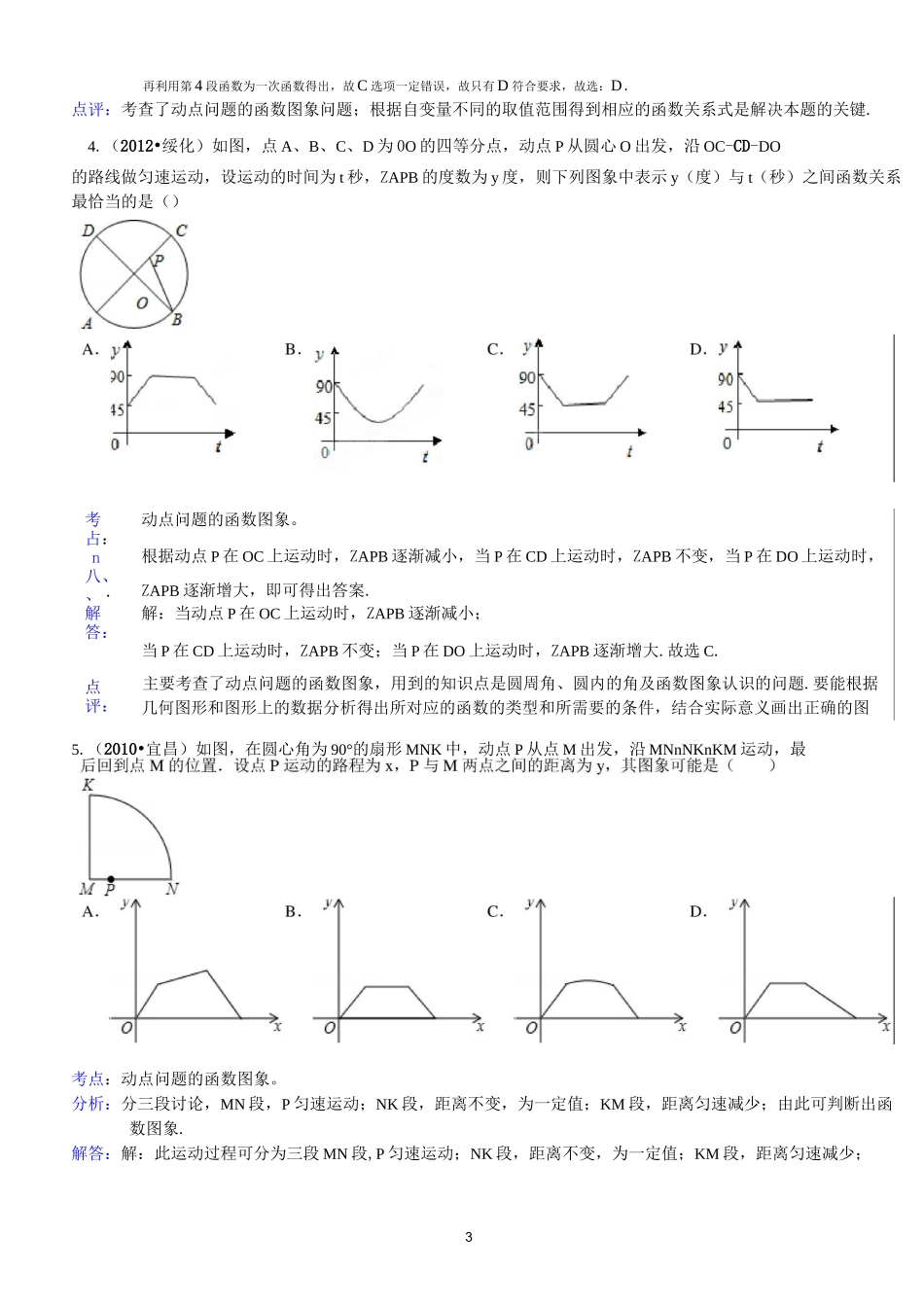
1动点问题的函数图象解答此类问题的策略可以归纳为三步:“看”、“写”、“选”。“看”就是认真观察几何图形,彻底弄清楚动点从何点开始出发,运动到何点停止,整个运动过程分为不同的几段,何点(时刻)是特殊点(时刻),这是准确解答的前提和关键;“写”就是计算、写出动点在不同路段的函数解析式,注意一定要注明自变量的取值范围,求出在特殊点的函数数值和自变量的值;“选”就是根据解析式选择准确的函数图像或答案,多用排除法。首先,排除不符合函数类形的图像选项,其次,对于相同函数类型的函数图像选项,再用自变量的取值范围或函数数值的最大和最小值进行排除,选出准确答案。一、选择题(共30小题)1.已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:GfC—DfEfFfH,相应的厶ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列四个结论中正确的个数有()①图1中的BC长是8cm;②图2中的M点表示第4秒时y的值为24;③图1中的CD长是4cm;④图1中的DE长是3cm;⑤图2中的Q点表示第8秒时y的值为33;⑥图2中的N点表示第12秒时y的值为18cm2.A.3B.4个C.5个D.6个考动点问题的函数图象。占八、、分①根据题意得:动点P在GC上运动的时间是2秒,又由动点的速度,可得GC和BC的长;析②③由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;:④根据题意得:动点P在DE上运动的时间是3秒,又由动点的速度,可得DE长;⑤根据图2中的Q点表示第8秒时,表示点P到达H点,即可得出y的值;⑥根据图2中的N点表示第12秒时,表示点P到达H点,即可得出厶ABP的面积;解解:①根据函数图象可以知:从0到2,y随x的增大而增大,经过了2秒,P运动了4cm,因而CG=4cm,BC=8cm;答②③P在CD段时,底边AB不变,高不变,因而面积不变,由图象可知CD=4cm,面积y=-;x6x8=24cm2;④根据函数图象可以知:经过了3秒,P运动了6cm,因而DE=6cm;⑤图2中的Q点表示第8秒时,表示点P到达F点,即可求出是y的值为36cm2.⑥图2中的N点表示第12秒时,表示点P到达H点,△ABP的面积是18cm2.则四个结论正确;故选B.点此题考查了动点问题的函数图象,要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,HEDG图图02F£1CnB2A.16B.15C.11D.5解y=x,莓冷+平…)C—I评结合实际意义得到正确的结论.2.如图1,在直角梯形ABCD中,动点P从点B出发,沿BC—CD运动至点D停止.设点P运动的路程为x,△APB的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是()考点:动点问题的函数图象。分析:根据函数图象横纵坐标表示的意义以及几何图形的特点分析即可.解答:解:动点P从直角梯形ABCD的直角顶点B出发,沿BC,CD的顺序运动,贝仏ABP面积y在AB段随x的增大而增大;在CD段,△ABP的底边不变,高不变,因而面积y不变化.由图2可以得到:BC=5,CD=6,△BCD的面积是丄x5x6=15.故选B.2点评:本题考查了动点问题的函数图象,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.3.(2012•嘉兴)如图,正方形ABCD的边长为a,动点P从点A出发,沿折线A—B—DfCfA的路径运动,回到点A时运动停止.设点P运动的路程长为长为x,AP长为y,则y关于x的函数图象大致是考点:动点问题的函数图象。_分析:根据题意设出点P运动的路程x与点P到点A的距离y的函数关系式,然后对x从0到2a+2•.迈a时分别进行分析,并写出分段函数,结合图象得出答案.解:设动点P按沿折线AfBfDfC^A的路径运动,•・•正方形ABCD的边长为a,・・・BD=2a,则当O^xVa时,当a(1+.2)