﹡2124一元二次方程的根与系数的关系VIP免费

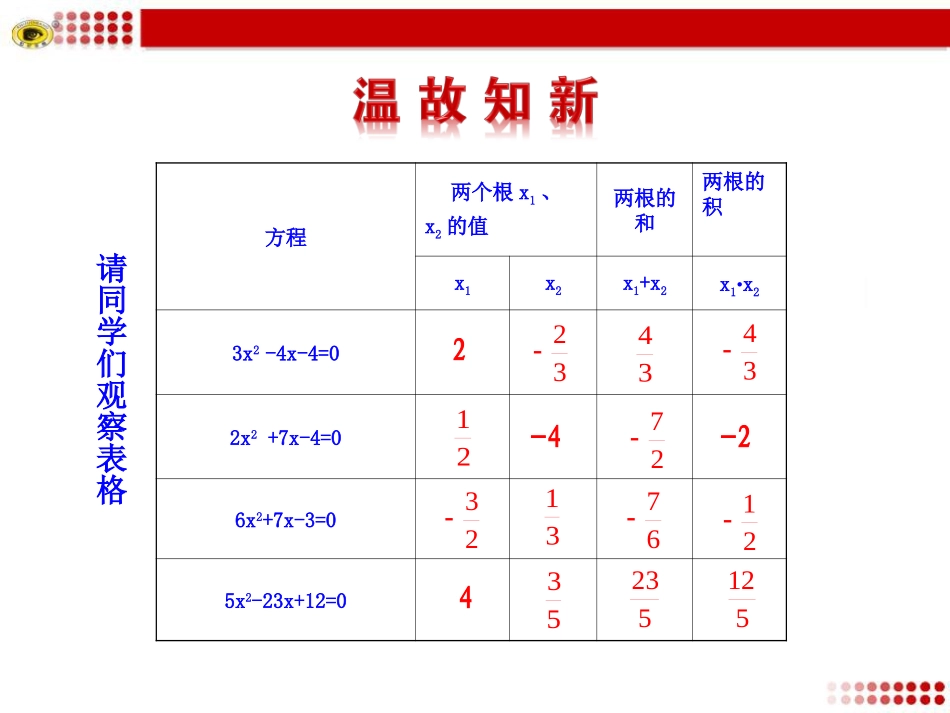
21.2.4一元二次方程的根与系数的关系﹡1.熟练掌握一元二次方程根与系数的关系.2.灵活运用一元二次方程根与系数的关系解决实际问题．3.提高学生综合运用基础知识分析解决较为复杂问题的能力．方程两个根x1、x2的值两根的和两根的积x1x2x1+x2x1·x23x2-4x-4=02x2+7x-4=06x2+7x-3=05x2-23x+12=02-4-24请同学们观察表格23434312723213761235235125请同学们猜想：对于任意的一元二次方程ax2+bx+c=0（a≠0）的两个实数根x1、x2，那么x1+x2，x1·x2与系数a，b，c的关系.x1+x2=x1.x2=abac如果一元二次方程ax2+bx+c=0（a≠0）的两个实数根是x1，x2那么x1+x2=，x1·x2=如果一元二次方程x2+px+q=0的两个根是x1，x2那么x1+x2=-px1·x2=qabac【归纳】【解析】设方程的另一个根是x1，那么2x1=∴x1=.又+2=答：方程的另一个根是，k的值是-7.∴k=-7【例1】已知方程5x2+kx-6=0的一个根是2，求它的另一个根及k的值.5653535k53【例题】x1+x2=，x1.x2=.【解析】设方程的两个根分别是x1、x2那么【例2】不解方程，求方程2x2+3x-1=0的两个根的（1）平方和（2）倒数和.（1）∵（x1+x2）2=x12+2x1.x2+x22∴x12+x22=（x1+x2）2-2x1.x2=（）2-2（）=（2）—+—=———=———=3x111x1.x2x1+x2x211232123214132321【例题】（1）x2-3x+1=0（2）3x2-2x=2（3）2x2+3x=0（4）3x2=21.下列方程两根的和与两根的积各是多少？（不解方程）32322332（1）3，1（2），（3），0（4）0，【跟踪训练】（1）x2-6x-7=0-1，7（2）3x2+5x-2=0，（3）2x2-3x+1=03，1（4）x2-4x+1=0，2.利用根与系数的关系，判断下列各方程后面的两个数是不是它的两个根?（口答）3232（√）（×）（×）（×）53231.（日照·中考）如果关于x的一元二次方程x2+px+q=0的两根分别为x1=2，x2=1，那么p，q的值分别是（）A.－3，2B.3，-2C.2，－3D.2，3【解析】选A，根据根与系数的关系得：x1+x2=-p=2+1=3，x1·x2=q=2，即p=－3，q=2.2.已知方程3x2-19x+m=0的一个根是1，它的另一个根是，m的值是.3.设x1,x2是方程2x2+4x-3=0的两个根，利用根与系数的关系，求下列各式的值.（1）（x1+1)(x2+1）（2）—+—x1x2x1x216316253144.（珠海·中考）已知x1=-1是方程x2+mx-5=0的一个根，求m的值及方程的另一根x2.【解析】由题意得：解得m=-4,当m=-4时，-1+x2=-(-4),x2=5所以方程的另一根x2=5.答：m=-4，x2=5.05)1()1(2m通过本课时的学习，需要我们：1.熟练掌握一元二次方程根与系数的关系.2.灵活运用一元二次方程根与系数的关系解决实际问题．认识一位巨人的研究方法，对于科学的进步并不比发现本身更少用处.科学研究的方法经常是极富兴趣的部分.——拉普拉斯