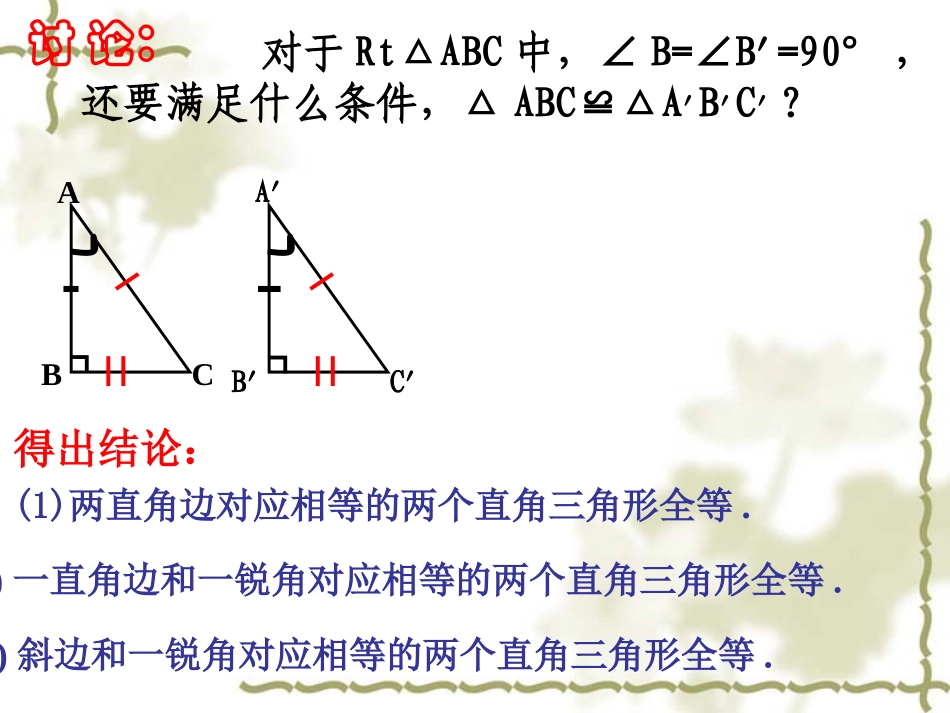
SSSASAAASSAS2、如图,Rt△ABC中,直角边、,斜边.ABCBCACAB1、判定两个三角形全等方法,,,,.我们把直角△ABC记作Rt△ABC.讨论:对于Rt△ABC中,∠B=∠B'=90°,还要满足什么条件,△ABC≌△A'B'C'?ABCA'B'C'得出结论:(1)两直角边对应相等的两个直角三角形全等.(2)一直角边和一锐角对应相等的两个直角三角形全等.(3)斜边和一锐角对应相等的两个直角三角形全等.┓┓如果添加AB=A'B',AC=A'C',能否证明△ABC≌△A'B'C'?ABCA'B'C'探究:MN●●画一个Rt△A'B'C',使AB=A'B',AC=A'C',1、画∠MB'N=90°;2、在射线B'M上截取B'A'=BA;3、以A'为圆心,AC长为半径画弧,交射线B'N于C',4、连接A'C'.斜边和一条直角边对应相等的两个三角形全等,数学语言:数学语言:AB=A´B´∵在Rt△ABC和Rt△A'B'C'中Rt△ABC≌RtA´B´C´△∴∟B´´C´´A´´∟BCA((HLHL))BC=B´C´简写为“斜边、直角边”或“HL”.直角三角形的判定方法想一想对于一般的三角形“SSA”不可以证明两个三角形全等ABCD但直角三角形作为特殊的三角形,SSA时也就是斜边、直角边判定判断两个直角三角形全等的方法有:(1):;(2):;(3):;(4):;SSSSASASAAAS(5):;HL如图:ACBC⊥,BDAD⊥,AC=BD.求证:BC=AD.ABCDO在RtACB△和RtBDA△中,则AB=BA(共公边)AC=BD.(已知)∴RtACBRtBDA(HL).△≌△∴BC=AD(全等三角形对应边相等).证明:ACBC⊥,BDAD⊥∴∠D=C=90°∠证明两个直角三角形全等,首先考虑用HL定理1.如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?CDAB解:在RtACB△和RtADB△中,AB=AB,AC=AD.∴RtACBRtADB(△△≌HL)∴BC=BD(全等三角形对应边相等).2.如图,AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证:AE=DF.CDFEABBDACE3.如图,C是路段AB的中点,两人从C同时出发以相同的速度分别沿两条直线行走,并同时到达D,E两地,此时,DA⊥AB,EB⊥AB,D、E到路段AB的距离相等吗?为什么?EDABBDECACECACBDCBDEDBDAB求证:且上一点是已知,,,:.4ABCED知识回顾:直角三角形全等的条件:1)定义(重合)法;SSS;SAS;ASA;AAS.2)解题中常用的4种方法3)HL直角三角形全等用一般不用如图,∠ACB=∠ADB=90,要证明△ABC≌△BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.(1)()(2)()(3)()(4)()ABDCAD=BC∠DAB=CBA∠BD=AC∠DBA=CAB∠HLHLAASAAS2.如图:AC⊥BC,BD⊥AD,AC=BD.求证:OA=OB.ABCDO1.如图,ABBC⊥,ADDC⊥,且AD=AB,求证:BC=DCCABD1.如图已知CE⊥AB,DF⊥AB,AC=BD,AF=BE,则CE=DF.请说明理由.第1题图2.如图,AB=AE,BC=ED,AFCD,B=E.⊥∠∠试说明:F是CD的中点.B第2题图FEDCBAEABCDFG3.如图:ABAC⊥,垂足为A,DEDF⊥于D,AB=DE,BF=EC,AD交BE于G,求证:AG=GD谈谈你本节课的收获谈谈你本节课的收获11、斜边、直角边(、斜边、直角边(HLHL)定理:斜边和)定理:斜边和一条直角边对应相等的两个三角形全等一条直角边对应相等的两个三角形全等22、证明两个直角三角形全等,不仅、证明两个直角三角形全等,不仅可以用可以用HLHL定理,还可以用定理,还可以用SASSAS、、ASAASA、、SSSSSS、、AASAAS定理来证明两个三角形定理来证明两个三角形全等全等