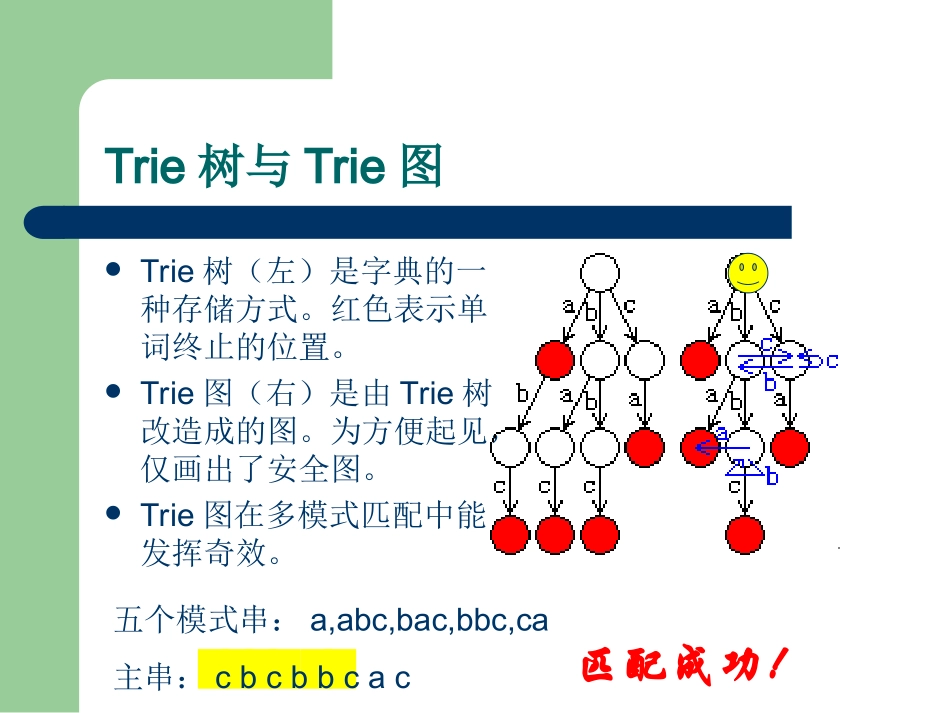
Trie图的构建、活用与改进山东省龙口一中王赟Trie树与Trie图Trie树(左)是字典的一种存储方式。红色表示单词终止的位置。Trie图(右)是由Trie树改造成的图。为方便起见,仅画出了安全图。Trie图在多模式匹配中能发挥奇效。五个模式串:a,abc,bac,bbc,ca主串:cbcbbcac匹配成功!Trie图的构建(例1)【例1】不良单词探测器【题目描述】给出一个词典,其中的单词为不良单词。单词均为小写字母。再给出一段文本,文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如,若rob是不良单词,那么文本problem含有不良单词。【输入】第一行为一个整数n,表示不良单词的个数。接下来n行是词典。下面一行为一个整数m,表示文本的行数。接下来m行是文本。【输出】如果文本包含不良单词,输出一行“Yes”,否则输出一行“No”。Trie图的构建(例1)【样例输入】1rob1internetproblemsolvingcontest【样例输出】Yes【备注】因本题只是用来讨论trie图的构建方法,故未给出数据范围。Trie图的构建(例1分析)判断文本是否包含不良单词可以一行一行地判断。而判断长为L的一行文本s是否含有不良单词可以这样进行:让i从1变化到L,依次判断s的前i个字符构成的字符串是否以不良单词结尾。然而,我们希望在判断s的前k个字符时,能够利用前k-1个字符的结果,即这两个状态间可以方便地进行转移。注意到trie树中的边正如一个个“方向标”,因此我们有了一个美好的设想:从根结点出发,沿着标有s[1]的边走一步,再沿标有s[2]的边走一步,一直这样走下去!Trie图的构建(例1分析)问题1:如果从当前走到的结点出发,没有需要走的边,该怎么办?“创造”一条这样的边!但我们不能同时创造一个结点,因此我们需要在已有的结点中找一个与我们想要走到的结点“等价”的结点。什么叫“等价”?先看这样一个问题:定义trie树中从根结点到某个结点的路径上的边上的字符连起来形成的字符串为这个结点的路径字符串。如果一个结点的路径字符串以不良单词结尾,那么称这个结点为危险结点,否则称之为安全结点。问题2:如何判断某个结点是否危险?Trie图的构建(计算结点的危险性)再给出几个定义:一个字符串去掉第一个字符后剩下的部分叫做它的后缀。一个字符串对应的结点是指在trie图中从根出发,依次沿该字符串的每个字符走一步所达到的结点。一个结点的路径字符串的后缀对应的结点称为它的后缀结点。显然根结点是安全结点。一个非根结点是危险结点的充要条件是:它的路径字符串本身就是一个不良单词,或它的路径字符串的后缀对应的结点是危险结点。于是问题2转化为:如何求一个结点的后缀结点?Trie图的构建(计算后缀结点)根结点的后缀结点是它本身。处于trie树第二层的结点的后缀结点也是根结点。对于再往下的某个结点,设它的路径字符串的最后一个字符为c,那么这个结点的后缀为从它在trie树中父结点的后缀结点出发,沿标有c的边走一步后到达的结点。(下文中称从x结点出发,沿标有字符c的边走一步到达的结点为x的c孩子)现在,问题2进一步转化为:如果它的父结点的后缀结点w没有c孩子怎么办呢?我们看到,两个问题已经合而为一了!Trie图的构建(两个问题的解决)我们假设w有这样一个c孩子(记作x),并且从x出发又繁衍出无数的子子孙孙。我们来判断x的危险性。显然x本身的路径字符串不是不良单词,且它的子孙的路径字符串也不是不良单词。因此以x为根的子树中任一结点y的危险性与y的后缀结点的危险性相同(回忆一下一个非根结点是危险结点的充要条件)。这也就是说,以x为根的子树与以x的后缀结点为根的子树是一模一样的。因此,我们把需要新建的从w指向x的边直接指向x的后缀结点,即w的后缀结点的c孩子即可。简言之,由于w本身的路径字符串既不是不良单词,又不是某个不良单词开头的一部分,所以它的首字母便没有用了!在这种情况下,w结点就等价于它的后缀结点。Trie图的构建(构建流程)按层次遍历trie树,同时:求出每个结点的危险性求出每个结点的后缀结点补齐由它出发的边补边的方法为:从根结点出发的补边指向根本身;...