抛物线的简单几何性质(1)VIP免费

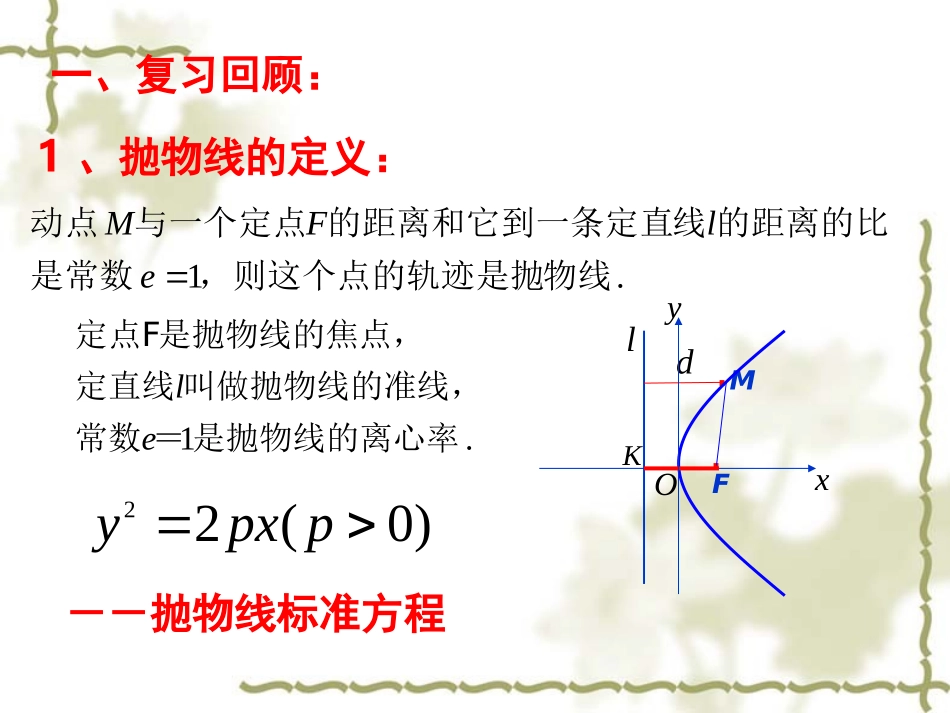
抛物线的简单几何性质(1)抛物线的简单几何性质(1)2024年12月30日一、复习回顾：.1物线，则这个点的轨迹是抛是常数的距离的比线的距离和它到一条定直与一个定点动点elFMl.FMd.1.le定点F是抛物线的焦点，定直线叫做抛物线的准线，常数＝是抛物线的离心率xOyK－－抛物线标准方程1、抛物线的定义：)0(22ppxy标准方程图形焦点准线)0(22ppxy)0(22ppyxxyoF..xyFo)0,2(pF.yxoF2px)2,0(pF.xoyF2py)0(22ppxy)0,2(pF2px)0(22ppyx)2,0(pF2py2、抛物线的标准方程：3、椭圆和双曲线的性质：方程性质)0(12222babyax)0,0(12222babyax图形范围bybaxa,Ryaxax,或对称性轴及原点对称关于yx,轴及原点对称关于yx,顶点坐标),0(),,0()0,(),0,(2121bBbBaAaA)0,(),0,(21aAaA叫短轴叫长轴2121,BBAA叫虚轴叫实轴2121,BBAA离心率)10(,eace)1(,eaceyox)0,2(pFP(x,y)一、抛物线的几何性质抛物线在y轴的右侧，当x的值增大时，︱y︱也增大，这说明抛物线向右上方和右下方无限延伸。1、范围由抛物线y2=2px（p>0）220pxy而0p0x所以抛物线的范围为0x(,)xy关于x轴对称(,)xy由于点也满足，故抛物线(p>0)关于x轴对称.(,)xyy2=2pxy2=2px2、对称性yox)0,2(pFP(x,y)定义：抛物线和它的轴的交点称为抛物线的顶点。yox)0,2(pFP(x,y)由y2=2px（p>0）当y=0时,x=0,因此抛物线的顶点就是坐标原点（0，0）。注:这与椭圆有四个顶点,双曲线有两个顶点不同。３、顶点4、离心率yox)0,2(pFP(x,y)抛物线上的点与焦点的距离和它到准线的距离之比，叫做抛物线的离心率，由抛物线的定义，可知e=1。下面请大家得出其余三种标准方程抛物线的几何性质。图形标准方程范围对称性顶点离心率)0(2ppxy2)0(2ppyx2)0(2ppyx2Ryx,0)0,0(Ryx,0Rxy,0Rxy,0)0,0()0,0()0,0(关于x轴对称，无对称中心关于x轴对称，无对称中心关于y轴对称，无对称中心关于y轴对称，无对称中心e=1e=1e=1e=1)0(2ppxy25、开口方向yox)0,2(pFP(x,y)抛物线y2=2px（p>0）的开口方向向右。pyxpyxpxypxy22222222+X，x轴正半轴，向右-X，x轴负半轴，向左+y，y轴正半轴，向上-y，y轴负半轴，向下特点：1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的,为1;思考：抛物线标准方程中的p对抛物线开口的影响.yox)0,2(pFP(x,y)4321-1-2-3-4-5-2246810y2=xy2=xy2=2xy2=4x21求它的标准方程。并且经过点标原点，轴对称，它的顶点在坐已知抛物线关于例),22,2(3x)0(2),22,2(2PPxyMx程为所以，可设它的标准方点点，并且经过轴对称，它的顶点在原解：因为抛物线关于222)22(2pPM，即在抛物线上，所以因为点xy42准方程是因此，所求抛物线的标三、例题选讲：变式：顶点在坐标原点，对称轴是坐标轴，并且经过点的抛物线有几条？求出它们的标准方程．(2,22)M(2,22)M的长。两点，求线段抛物线相交于且与的焦点经过抛物线的直线斜率为例ABBAFxyl,,4142xyOFABB’A’,12,2pp解：由题意可知，.1:xl准线.,,),,(),,(2211BAddlBAyxByxA的距离分别为准线到设,1,121xdBFxdAFBA由抛物线的定义可知221xxBFAFAB所以X1+X2=？整体运算分析：运用分析：运用抛物线的定抛物线的定义和平面几义和平面几何知识来证何知识来证比较简捷．比较简捷．xyOFBAxyOFBADCxyEOFBADCHxyEOFBADCHxyEOFBADCHxyEOFBADCHxyEOFBADCH拓展：过抛物线y2=2px的焦点F任作一条直线m，交这抛物线于A、B两点，求证：以AB为直径的圆和这抛物线的准线相切．证明：如图．xyEOFBADCH所以EH是以AB为直径的圆E的半径，且EH⊥l，因而圆E和准线l相切．设AB的中点为E，过A、E、B分别向准线l引垂线AD，EH，BC，垂足为D、H、C，则｜AF｜＝｜AD｜，｜BF｜＝｜BC｜∴｜AB｜＝｜AF｜＋｜BF｜＝｜AD｜＋｜BC｜=2｜EH｜思考1:(课本第76页例6)已知抛物线的方程为24yx,直线l过定点(2,1)P,斜率为k,k为何值时,直...