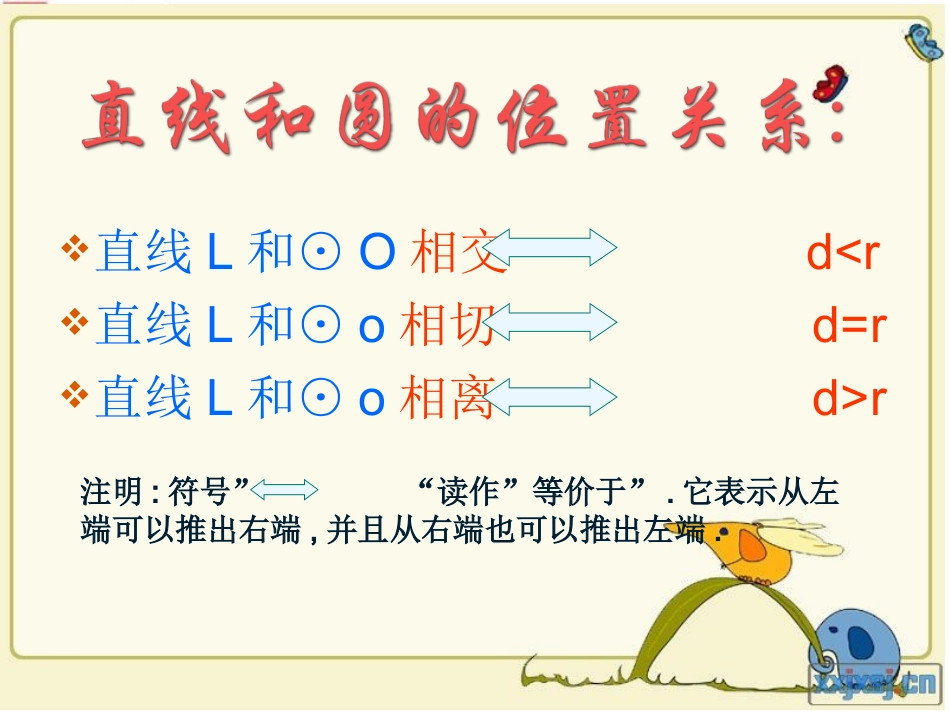
思考:判定直线与圆的位置关系的方法有____种:(1)根据定义,由________________的个数来判断;(2)根据性质,由_______________________________的关系来判断。在实际应用中,常采用第二种方法判定。两直线与圆的公共点圆心到直线的距离d与半径r思考:判定直线与圆的位置关系的方法有____种:(1)根据定义,由________________的个数来判断;(2)根据性质,由_______________________________的关系来判断。直线L和⊙O相交dr注明:符号”“读作”等价于”.它表示从左端可以推出右端,并且从右端也可以推出左端.如图,直线l是圆O的切线,切点为A,圆O的半径为r.⑴圆心O到切线l的垂线段的长度等于什么?圆心O到切线l的垂线段的长度是圆心O到切线l的距离d,从而它等于半径r.·OAl探究⑵由于圆心O到切线l垂线段的长度等于半径OA的长度,且点A在切线l上,因此圆心O到切线l的垂线段就是________.切线的性质定理:圆的切线垂直于过切点的半径.从第⑵点的结论得出:半径·OAl【思考】1.如何用语言叙述上述结论?2.如何用几何语言表示你得出的结论?切线的性质定理:切线的性质定理:圆的切线垂直于过切点的半径.辅助线作法:连接圆心与切点可得半径与切线垂直。即“连半径,得垂直”。几何语言:在⊙O中∵直线l切☉O于点T,∴OT⊥l.如图,直线l是圆O的切线,切点为A,∠OBA=40°,求∠AOB.·OABl解:由于线段OA是过切点的半径,因此OA⊥l,从而∠OAB=90°,于是∠AOB=90°-40°=50°40°例1大圆的弦AB所在直线是小圆的切线,切点为C,···ABO练习求证:C是线段AB的中点.1.如图,这是手表的圆形表盘,两个圆的圆心都是O,C∴C为AB的中点证明:两个同心圆.连接OA,OB∴△OAB为等腰三角形OA=OBC为切点,OC⊥AB即OC为△ABO的高,∴OC为△ABO的中线A组1BAOPC练习2、PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,求∠ACB的度数.解::连结OAOB∵PA、PB是⊙O的切线∴OA⊥PAOB⊥PB又∵∠APB=40°AOB=140°∴∠又∵弧AB=弧AB∴∠AOB=2ACB∠∴∠ACB=70°PAO2、已知P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sinAPO=________∠1、已知:如图:在△ABC中,AC与⊙O相切于点C,BC过圆心,∠BAC=63°,则∠ABC=--------。27°3、已知:如图:AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,∠OBA=---------。36°531题2题3题如图,在⊙O中经过半径OA的外端点A作直线l⊥OA,则(1)圆心O到直线l的距离是多少?这时圆心O到直线l的距离就是⊙O的半径.Alo(2)直线l和⊙O有什么位置关系?由d=r直线l是⊙O的切线.共同探究2:ALo切线的判定定理切线的判定定理::经过半径的外端并且垂经过半径的外端并且垂直于这条半径的直线是圆的切线。直于这条半径的直线是圆的切线。几何符号表达几何符号表达::∵∵OAOA是是⊙⊙OO半径,半径,OA⊥LOA⊥L于于点点AA∴∴LL是⊙是⊙OO的切线。的切线。AloALo说明:⑴如图,定理的题设是:一条直线l满足两个条件:①经过半径OA的外端点A;②垂直这条半径OA。结论:这条直线l是圆的切线。即直线lOA⊥于A,则l为⊙O的切线。⑵定理题设中的两个条件“经过半径的外端”和“垂直于这条半径”缺一不可,否则就不是圆的切线。〖例2〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。OOBBAACC分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可。证明:连结OC(如图)。∵OA=OB,CA=CB,∴OC是等腰三角形OAB底边AB上的中线。∴AB⊥OC。∵OC是⊙O的半径∴AB是⊙O的切线。〖例3〗已知:已知:OO为∠为∠BACBAC平分线上一点,平分线上一点,OD⊥ABOD⊥AB于于D,D,以以OO为圆心,为圆心,ODOD为半径作⊙为半径作⊙OO。。求证:⊙求证:⊙OO与与ACAC相切。相切。OOAABBCCEEDD证明:过O作OE⊥AC于E。∵AO平分∠BAC,OD⊥AB∴OE=OD∵OD是⊙O的半径∴AC是⊙O的切线。分析:要证的AC线与圆没有公共点,过圆心做AC的垂线OE,证OE等于半径OD小结例2与例3的证法有何不同?(1)如果已知直线经过圆上一点(直线与圆有公共点),则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。OOBBAACCOOAABBCCEEDD作业