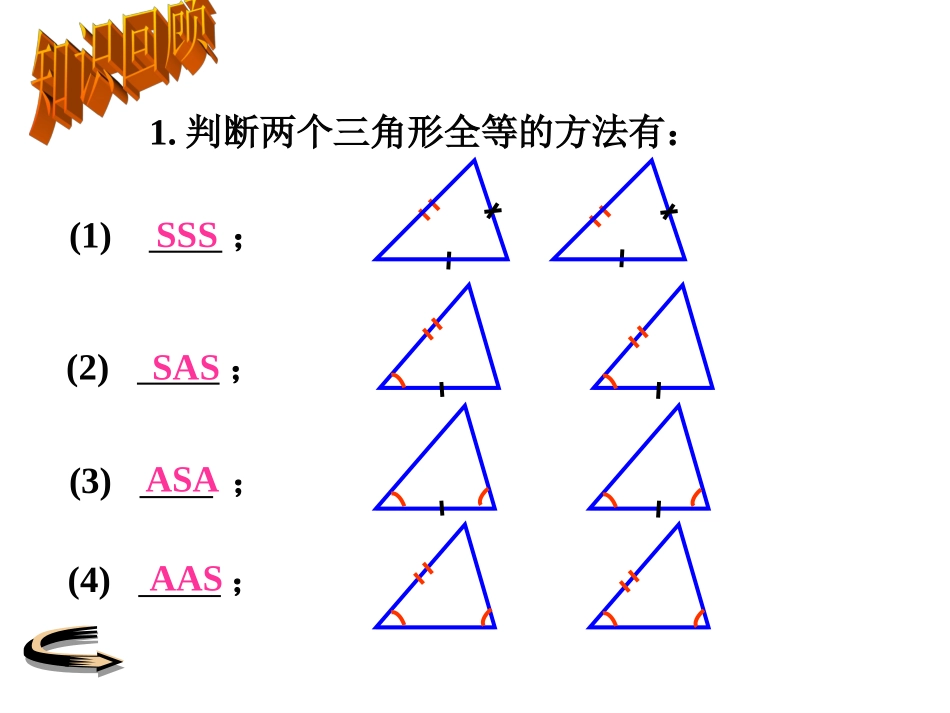
1.判断两个三角形全等的方法有:(1);(2);(3);(4);SSSSASASAAAS2、全等三角形的性质:两三角形全等,则对应边,对应角,3、如图,若△ABC≌△DEF,则,,,,,。相等相等∠A=D∠∠B=E∠∠C=F∠AC=DFBC=EFAB=DEABCDFE1.请你在下列各图中,以最快的速度画出一个三角形,使它与△ABC全等,比比看谁快!ABCACBACBD′DDEDEE在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离。由于没有任何测量工具,我八路军战士为此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功。这位聪明的八路军战士的方法如下:战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。ACBD?你觉得他测得的距离准确吗?说明其中的理由。BC=DC()ACBD?理由:在△ACB与△ACD中,∠BAC=DAC∠AC=AC(公共边)∠ACB=ACD=90°∠△ACBA△CD(ASA)全等三角形的对应边相等步测距离碉堡距离小明在上周末游览风景区时,看到了一个美丽的池塘,他想知道最远两点A、B之间的距离,但是他没有船,不能直接去测。手里只有一根绳子和一把尺子,他怎样才能测出A、B之间的距离呢?把你的设计方案在图上画出来,并与你的同伴交流你的方案,看看谁是方案更便捷。AB●●A、B间有多远呢?AB●●●CED在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC到E,使CE=BC,连接ED。则只要测出ED的长就可以知道AB的长了。理由如下:在△ACB与△DCE中,∠BCA=∠ECDAC=CDBC=CE△ACBDCE≌△(SAS)AB=DE()全等三角形的对应边相等·在AB的垂线BF上取两点C,D,使BC=DC,过点D作出BF的垂线DG,并在DG上找一点E,使A,C,E在一条直线上,这时测得DE的长是A,B间的距离。BEAGCDF·CDF·鸽子距离地面有多高呢?ADEFOG●C1.如图要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDCAB≌△C,得ED=AB,因此,测得ED的长就是AB的长。判定△EDCABC≌△的理由是()A、SSSB、ASAC、AASD、SASBA●●DCEFB2.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO应满足下列的哪个条件?()A、AO=COB、BO=DOC、AC=BDD、AO=CO且BO=DODODCBAABCEDF3.3.如图,如图,AA、、BB两座两座建筑物分别位于马路建筑物分别位于马路的两边,你能设计一的两边,你能设计一个方案测得它们之间个方案测得它们之间的距离吗?的距离吗?···沿马路画一条与马路平行的射沿马路画一条与马路平行的射线线BCBC,在,在BCBC上截取上截取BD=DEBD=DE,过,过EE作作EFAB∥EFAB∥,使,使AA、、DD、、FF在同一直在同一直线是,则线是,则EFEF的长就是建筑物的长就是建筑物AA、、BB之间的距离,你能说明理由吗?之间的距离,你能说明理由吗?4.如图是挂在墙上的一面大镜子,上面有两点A、B。小明想知道A、B两点之间的距离,但镜子挂得太高,无法直接测量,旁边又没有梯子,只有一根长度比圆的直径稍长点的竹竿和一把卷尺。小明做了如下操作:在他够的着的圆上找到一点C,接下去小明却忘了应该怎么做?你能帮助他完成吗?A··BEDC●在一座楼相邻两面墙的外部有两点A、C,如图所示,请设计方案测量A、C两点间的距离。(试用两种方法)AC?AC在一座楼相邻两面墙的外部有两点A、C,如图所示,请设计方案测量A、C两点间的距离。(试用两种方法)?BBDD1、知识:利用三角形全等测距离的目的:变不可测距离为可测距离。依据:全等三角形的性质。关键:构造全等三角形。2、方法:(1)延长法构造全等三角形;(2)垂直法构造全等三角形。3、数学思想:树立用三角形全等构建数学模型解决实际问题的思想。一分耕耘,一分收获。