修改正弦定理课件,,,VIP免费

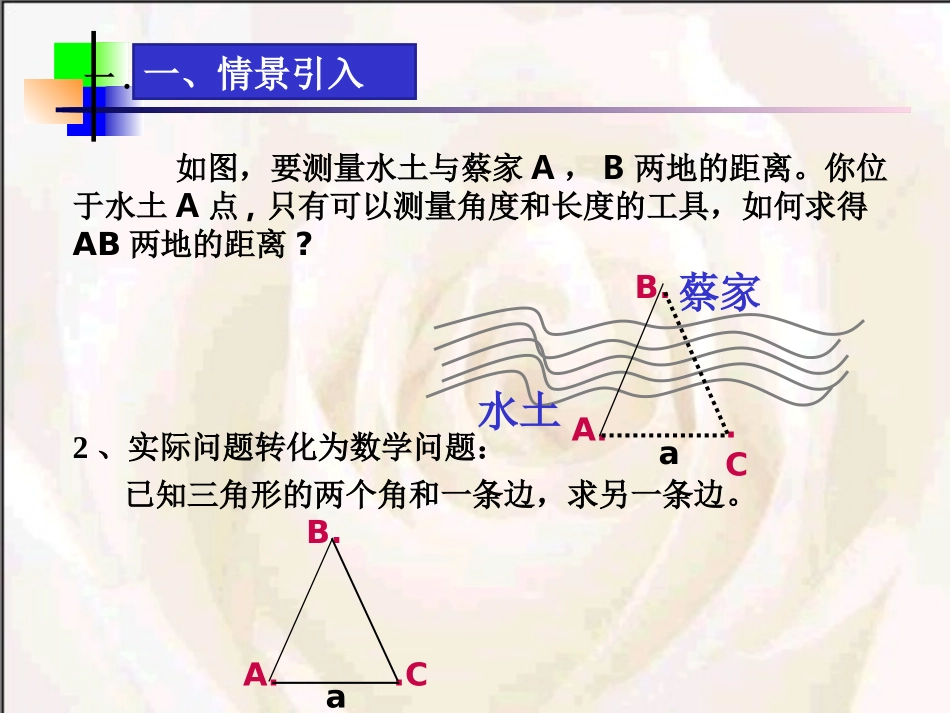
第8章:解三角形田茜2014.3.6一.2、实际问题转化为数学问题：如图，要测量水土与蔡家A，B两地的距离。你位于水土A点,只有可以测量角度和长度的工具，如何求得AB两地的距离?B.A..CaB.A..Ca已知三角形的两个角和一条边，求另一条边。一、情景引入蔡家水土ABCbacD1hCcBbAasinsinsin二、定理的推导cCbBaASCabSBacSAbcSAbhchSABCsinsinsinsin,sin21,sin21sin2111同理可得，CcBbAasinsinsin正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即含三角形的三边及三内角定理结构特征:三、得出结论剖析定理、加深理解sinsinsinabcABC1、A+B+C=π正弦定理：2、一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫解三角形剖析定理、加深理解具体可以解决三角形中的什么问题？sinsinsinabcABC正弦定理：例1在已知解三角形.ABC0030,135,2ABa四、学以致用,15oC解:由正弦定理sinsinsinabcABC得ooocb15sin135sin30sin222212b,22b将a=2改为c=2，结果如何？26,426212cc,42622212cb探究课题引入时问题(2)的解决方法ABCbbsinβAB=sin(α+β)c?)sin(sin,)sin(sincbcb)sin(sin),(BB例2、已知a=16，b=，A=30°.解三角形解：由正弦定理BbAasinsin得231630sin316sinsinaAbB所以Ｂ＝60°,或Ｂ＝120°当时Ｂ＝60°C=90°.32cC=30°.16sinsinACac316当Ｂ＝120°时)180,0(ooB变式ooBBBBbAa30,21sin,sin245sin2sinsin2,2,45baAo1.在△ABC中，，求B.解:或O150B.3018045150ooooB2.在△ABC中，求B.解：由正弦定理BbAasinsin得〉1所以：无解34,4,60baAo23sinsin3460sin4BBo正弦定理可以解决三角形中的问题：①已知两角和一边，求其他角和边②已知两边和其中一边的对角(解的个数一解,两解,无解)sinsinsinabcABC正弦定理：在△ABC中，,30,2oAb分别计算各条件下B的值21)4(13)3(22)2(1)1(aaaa练一练•正弦定理sinsinsinabcABC(1)已知两角及任意一边，可以求出其他两边和另一角；(2)已知两边和其中一边的对角，可以求出三角形的其他的边和角.(可能有一解、二解、无解）（3）解决实际生活中的问题小结:五、归纳小结思想方法:数形结合•主要应用课后探究:sinsinsinabckABC那么这个k值是什么呢?你能用一个和三角形有关的量来表示吗?作业：课后练习题