二次根式复习课VIP免费

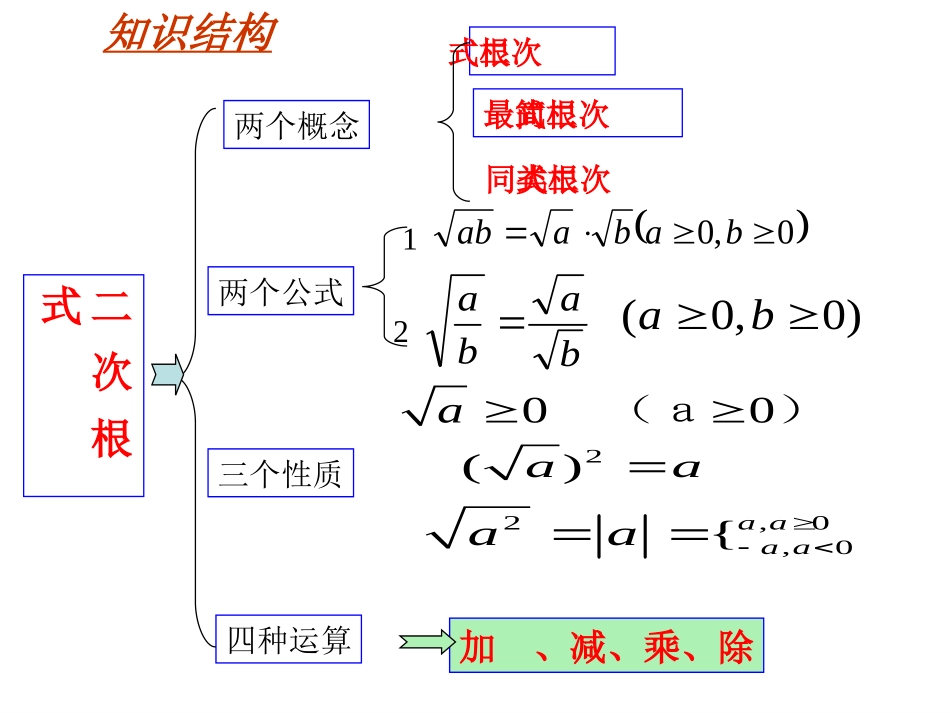
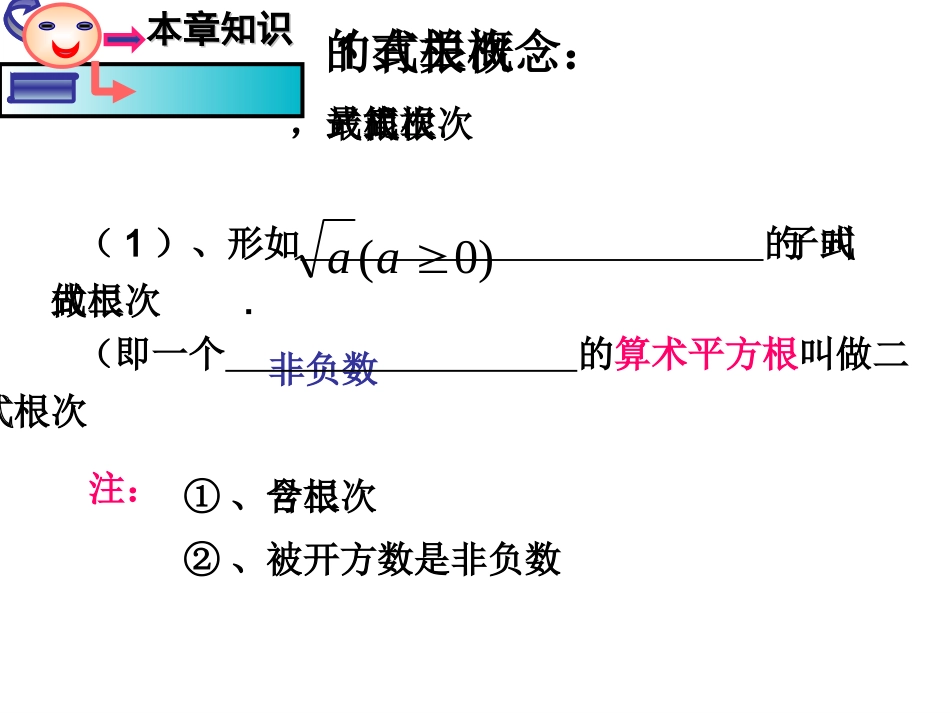
二县直九年级数学组二次根式两个概念两个公式三个性质四种运算baba)0,0(ba0,0babaab12加、减、乘、除知识结构2()aa2,0,0{aaaaaa00a（ａ）二次根式最简二次根式同类二次根式（1）、形如的式子叫做二次根式.本章知识本章知识非负数（二次根式，最简二次根式）注：①、含二次根号②、被开方数是非负数（即一个的算术平方根叫做二次根式）1、二次根式的有关概念：)0(aa一、二次根式的意义例1、找出下列各根式：中的二次根式。327)4(4122aa)21(12aa22a练习．下列各式中那些是二次根式？练习．下列各式中那些是二次根式？那些不是？为什么？那些不是？为什么？153a100x3522ab21a144221aa⑧⑧⑦⑦⑥⑥⑤⑤④④①①②②③③（2）、二次根式有意义的条件：本章知识本章知识0:aa中，在即被开方数大于或等于零例2：x为何值时，下列各式在实数范围内有意义。1)1(xx31)2(322)3(x123)4(x01x1x012x21x0322x31x031x31x为什么不取“=”号练习：x为何值时，下列各式在实数范围内有意义。x31)1(2)5()3(x1)4(2x123)5(xx12)6(0)6(5)7(xxxx31)2(确定二次根式中被开方数所含字母的取值范围.1.当X_____时，有意义。x33.求下列二次根式中字母的取值范围x315x2.(2006.青岛)+a44a有意义的条件是___________2162)1(取值范围是的中字母下列式子xxx?2、已知求算术平方根。977xxy2)64(xy的值。求、已知函数xyxxxy,1-2-245、已知x、y是实数，且求3x+4y的值。214422xxxy①、被开方数不含分母；（3）、满足下列两个条件的二次根式，叫做最简二次根式：②、被开方数中不含能开得尽方的因数或因式。本章知识本章知识练习：判断下列各式中哪些是最简二次根式，哪些不是？12)1(5.1)2(21)3(7)4(练习：把下列二次根化为最简二次根式。12)1(23)2(3432222326化简二次根式的方法：（1）如果被开方数是整数或整式时，先因数分解或因式分解,然后利用积的算术平方根的性质,将式子化简。（2）如果被开方数是分数或分式时,先利用商的算术平方根的性质,将其变为二次根式相除的形式,然后利用分母有理化,将式子化简。例1：把下列各式化成最简二次根式例2：把下列各式化成最简二次根式22164)2(54)1(aa(a≥0)(x>0)xyx2)2(2114)1(2、二次根式的性质a、)1()0(a2)()2(a、2)3(a、本章知识本章知识a)0(a0)0(a)0(a)0(aaa0a二次根式的非负性的应用.4.已知：+=0,求x-y的值.yx24x5.已知x,y为实数,且+3(y-2)2=0,则x-y的值为()A.3B.-3C.1D.-11xD的取值范围是，则）（若aaa22.62计算2)(aa)0(a例1、把下列各式在实数范围内分解因式:54)1(2x9)2(4a103)3(2a96)4(24aa1、式子成立的条件是（）1)1(2aa1.aA1.aB1.aC1.aDD的取值范围是，则）（若aaa22.62的应用a2a2、已知ab<0，则代数式可化为（）ba2CA.B.C.D.babababa3、已知三角形的三边长分别是a、b、c，且，那么等于（）A、2a-bB、2c-bC、b-2aD、b-2Cca2)(bcaacD221323.1）（）（化简：441.222aaa）（3、实数在数轴上的位置如图示，化简|a-1|+2)2(a。1244、请计算、请计算a=a=，，b=b=，，求求aa22b-abb-ab22的值的值12练习:化简23-11232-22223322-14222725727-33本章知识本章知识3.二次根式的运算：二次根式乘法法则：0)b,0(baaba二次根式除法法则：0)b,0(babaa二次根式的加减：类似于合并同类项，把相同二次根式的项合并.（3）合并被开方数相同的二次根式。一化二找三合并二次根式加减法的步骤：（1）将每个二次根式化为最简二次根式；（2）找出其中被开方数相同的二次根式；练一练（可要细心哟）48212335)1()622()622)(4(32)274483)(5(2)5048)(2()31312(27)3(11．要使下列式子有意义，求字母Ｘ．要使下列式子有意义，求字母Ｘ的取值范围的取值范围（１）（１）3x...