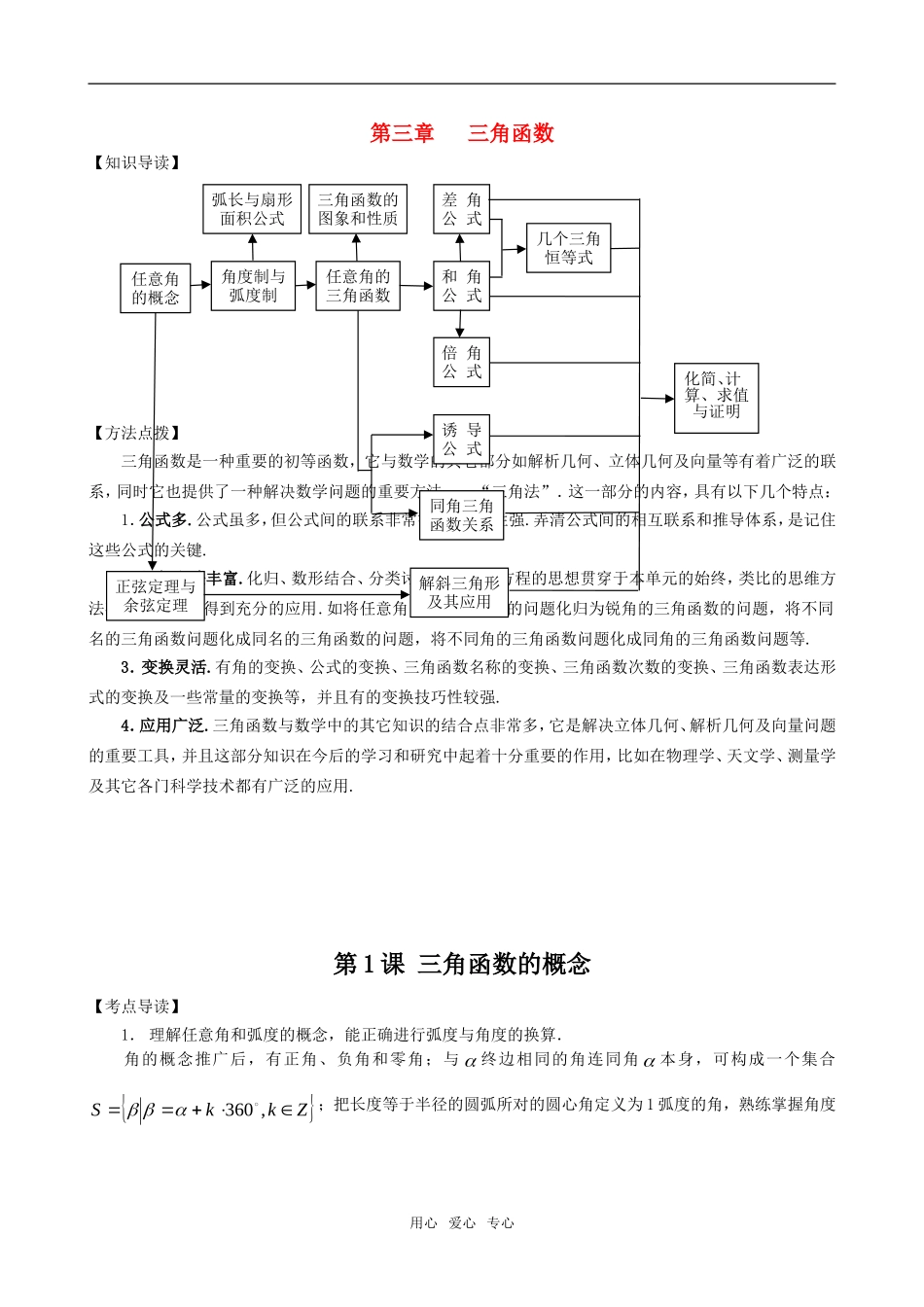
第三章三角函数【知识导读】【方法点拨】三角函数是一种重要的初等函数,它与数学的其它部分如解析几何、立体几何及向量等有着广泛的联系,同时它也提供了一种解决数学问题的重要方法——“三角法”.这一部分的内容,具有以下几个特点:1.公式多.公式虽多,但公式间的联系非常密切,规律性强.弄清公式间的相互联系和推导体系,是记住这些公式的关键.2.思想方法丰富.化归、数形结合、分类讨论和函数与方程的思想贯穿于本单元的始终,类比的思维方法在本单元中也得到充分的应用.如将任意角的三角函数值的问题化归为锐角的三角函数的问题,将不同名的三角函数问题化成同名的三角函数的问题,将不同角的三角函数问题化成同角的三角函数问题等.3.变换灵活.有角的变换、公式的变换、三角函数名称的变换、三角函数次数的变换、三角函数表达形式的变换及一些常量的变换等,并且有的变换技巧性较强.4.应用广泛.三角函数与数学中的其它知识的结合点非常多,它是解决立体几何、解析几何及向量问题的重要工具,并且这部分知识在今后的学习和研究中起着十分重要的作用,比如在物理学、天文学、测量学及其它各门科学技术都有广泛的应用.第1课三角函数的概念【考点导读】1.理解任意角和弧度的概念,能正确进行弧度与角度的换算.角的概念推广后,有正角、负角和零角;与终边相同的角连同角本身,可构成一个集合ZkkS,360;把长度等于半径的圆弧所对的圆心角定义为1弧度的角,熟练掌握角度用心爱心专心任意角的概念角度制与弧度制任意角的三角函数弧长与扇形面积公式三角函数的图象和性质和角公式差角公式几个三角恒等式倍角公式同角三角函数关系诱导公式正弦定理与余弦定理解斜三角形及其应用化简、计算、求值与证明与弧度的互换,能运用弧长公式rl及扇形的面积公式S=lr21(l为弧长)解决问题.2.理解任意角的正弦、余弦、正切的定义.角的概念推广以后,以角的顶点为坐标原点,角的始边为x轴的正半轴,建立直角坐标系,在角的终边上任取一点(,)Pxy(不同于坐标原点),设OPr(220rxy),则的三个三角函数值定义为:sin,cos,tanyxyrrx.从定义中不难得出六个三角函数的定义域:正弦函数、余弦函数的定义域为R;正切函数的定义域为{|,,}2RkkZ.3.掌握判断三角函数值的符号的规律,熟记特殊角的三角函数值.由三角函数的定义不难得出三个三角函数值的符号,可以简记为:一正(第一象限内全为正值),二正弦(第二象限内只有正弦值为正),三切(第三象限只有正切值为正),四余弦(第四象限内只有余弦值为正).另外,熟记0、6、4、3、2的三角函数值,对快速、准确地运算很有好处.4.掌握正弦线、余弦线、正切线的概念.在平面直角坐标系中,正确地画出一个角的正弦线、余弦线和正切线,并能运用正弦线、余弦线和正切线理解三角函数的性质、解决三角不等式等问题.【基础练习】1.885化成2(02,)kkZ的形式是.2.已知为第三象限角,则2所在的象限是.3.已知角的终边过点(5,12)P,则cos=,tan=.4.tan(3)sin5cos8的符号为.5.已知角的终边上一点(,1)Pa(0a),且atan,求sin,cos的值.解:由三角函数定义知,1a,当1a时,2sin2,2cos2;当1a时,2sin2,2cos2.【范例解析】用心爱心专心第二或第四象限正例1.如图,,分别是终边落在OM,ON位置上的两个角,且30,300.(1)求终边落在阴影部分(含边界)时所有角的集合;(2)终边落在阴影部分,且在区间[0,360]时所有角的集合;(3)求始边在OM位置上,终边在ON位置上所有角的集合.解:(1){6036030360,}kkkZ;(2){030}{300360};(3)270,{270360,}kkZ.点评:三角函数中应注意文字语言与符号语言的转化;第(3)问要注意角的方向.例2.(1)已知角的终边经过一点(4,3)(0)Paaa,求2sincos的值;(2)已知角的终边在一条直线3yx上,求s...