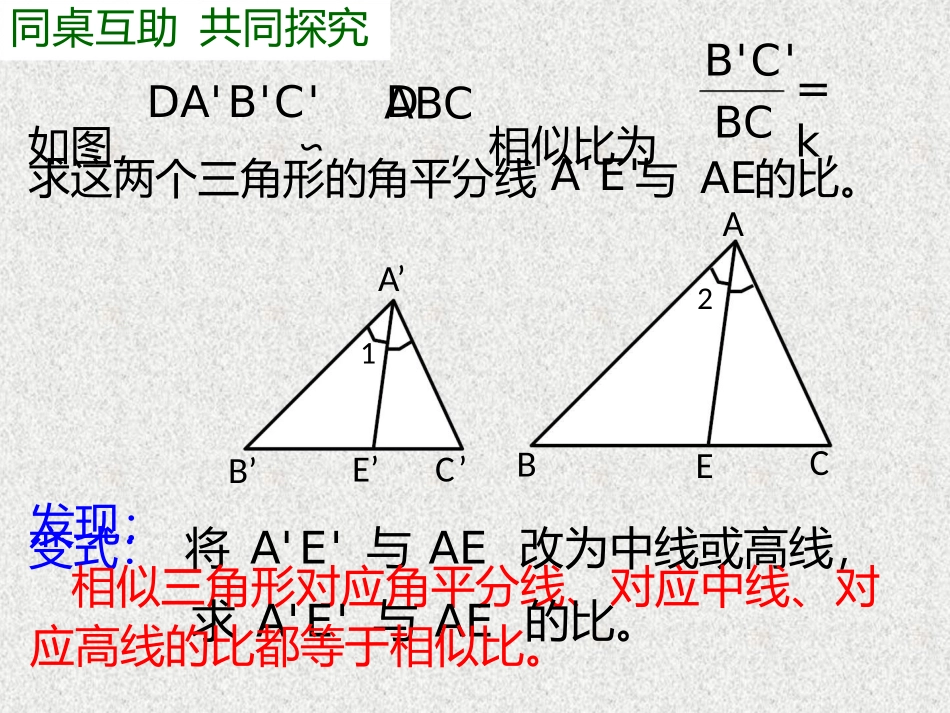
4.5相似三角形的性质及其应用(1)温故知新回顾相似三角形的定义、判定方法和基本性质:◆相似三角形的定义:对应角相等,对应边成比例的两个三角形,叫做相似三角形。◆相似三角形的基本性质:相似三角形的对应角相等,对应边成比例。同桌互助共同探究B'C'=kDA'B'C'D如图,∽,相似比为,ABCBCA'E'AE求这两个三角形的角平分线与的比。AA’21BECB’E’C’发现:变式:将A'E'与AE改为中线或高线,相似三角形对应角平分线、对应中线、对求A'E'与AE的比。应高线的比都等于相似比。探求新知A已知:如图,BE、CF是△ABC的两条中线,P是它们的交点。FEEPFP1==BPCP2求证:PBC探求新知如图,△ABC的两条中线BE、CF交于P点,那么BC边上的中线AG是否也经过P点呢?AFEP’BGC探求新知如图,△ABC的两条中线BE、CF交于P点,那么BC边上的中线AG是否也经过P点呢?AEP’BGC探求新知A★重心的定义:三角形三条中线的交点叫做三角形的重心。FEPBGC★重心的性质:三角形的重心分每一条中线成1:2的两条线段。实验观察比较◆物理意义上的重心与数学意义上的重心有什么关系?(1)用悬挂法确定三角形纸板的重心;(2)观察重力作用线所在的位置,有何发现?过对边的中点◆重力作用线_____________;三角形三条中线◆三角形物理意义的重心位于_____________的交点,和数学意义上的重心位置_相__重__合__。学以致用1.已知:如图,在△ABC中,E、F、G分别是AB、AC、BC上的点,EF∥BC,BG=CG,AG交EF于点P。求证:EP=FP。AEFPCBG学以致用2.如图,AG为△ABC的一条中线,P为△ABC的重心,EF∥BC,交AB、AC于点E、F,交AG于点P。求EF与BC的比。AEFPCBG学以致用3.如图,在△ABC中,中线AP、BE相交于点F,EG∥BC,交AP于点G,求AG与GF的比。AEGFBPC感悟与收获本节课我有什么收获?作业布置1.配套作业本;2.课后延伸:请借助互联网或查阅相关资料,探索用不同的方法推导“三角形的三条中线交于同一点”。