新人教版(B)高中数学必修1指数与指数函数教案VIP免费

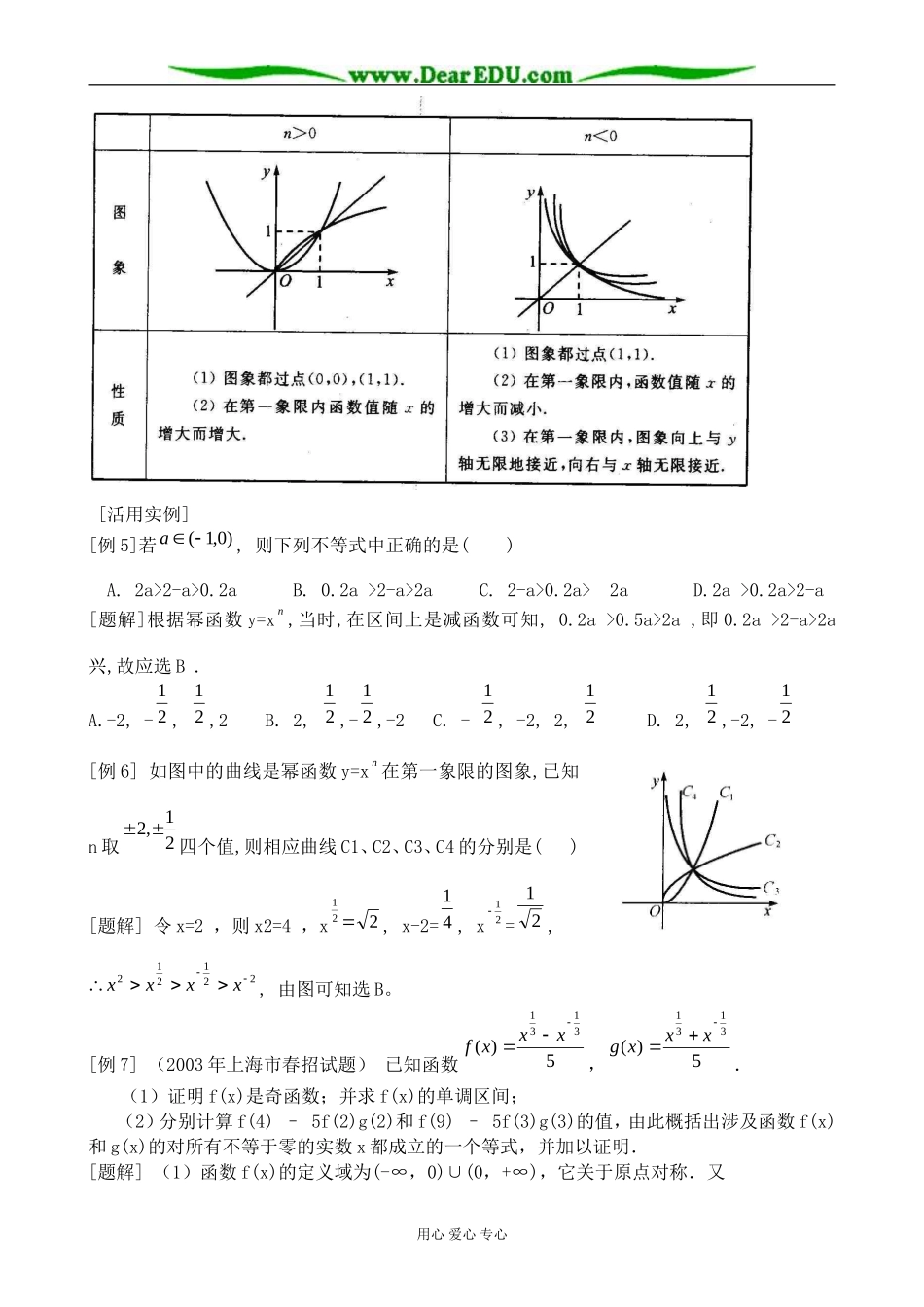
指数与指数函数知识网络指数与指数函数结构简图画龙点晴概念a的n次方根：若),1(Nnnaxn则x叫做a的n次方根.当n为奇数时，正数的n次方根为正数，负数的n次方根为负数记作：nax;当n为偶数时正数的n次方根有两个（互为相反数）记作:nax;负数没有偶次方根,0的任何次方根为0.根式:式子na叫做根式，n叫做根指数，a叫做被开方数；当n为奇数时，aann；当n为偶数时，)0()0(||aaaaaann。[活用实例][例1]写出使下列等式成立的x的取值范围：(1)313133xx;(2)5)5()25)(5(2xxxx.[题解](1)只须31x有意义，即x¹3∴x的取值范围是(∞,3)∪(3,+∞);(2) 55)5()5()25)(5(22xxxxxx∴5)5(55xxxx成立的充要条件是0555550505xxxxxxx或即：或∴x的取值范围是[5,5]。[例2]化简323213312xxxxxy.[题解] 1)1(13333323xxxxx用心爱心专心)1(1)1(11122xxxxxxx∴)1(2)1(2xxxy.分数指数幂：由n次根式定义,naamnm的是次方根，即：nmnmaa，同样规定：)1*,,0(1nNnmaaanmnm且;0的正分数指数幂等于0，0的负分数指数幂没有意义.整数指数幂的运算性质推广到有理指数幂：),0,0()(),,0()(),,0(QrbabaabQsraaaQsraaaarrrrssrsrsr[活用实例][例3]计算下列各式：（1）3263425.0031)32()32(28)67(5.1；（2）33323323134)21(428aabbababaa[题解]（1）原式=1102742323222)32(131224143）（３１;（2）原式=ababaaabaabbaabaa8)8(242)8(313131313231313231.[例4]已知a32+b32=4，x=a+3a31b32，y=b+3a32b31，求证：(x+y)32+(x-y)32为定值。[题解]因为x+y=a+3a31b32+3a32b31+b=(a31+b31)3，所以(x+y)32=(a31+b31)2=a32+2a31b31+b32，类似可得(x-y)32=(a31-b31)2=a32-2a31b31+b32，所以原式=2（a32+b32）=24=8（定值）。幂函数:函数y=xn叫做幂函数,其中x是自变量,n常数,n.R幂函数的图象和性质:用心爱心专心[活用实例][例5]若)0,1(a,则下列不等式中正确的是()A.2a>2-a>0.2aB.0.2a>2-a>2aC.2-a>0.2a>2aD.2a>0.2a>2-a[题解]根据幂函数y=xn,当时,在区间上是减函数可知,0.2a>0.5a>2a,即0.2a>2-a>2a兴,故应选B.A.-2,-21,21,2B.2,21,-21,-2C.-21,-2,2,21D.2,21,-2,-21[例6]如图中的曲线是幂函数y=xn在第一象限的图象,已知n取21,2四个值,则相应曲线C1、C2、C3、C4的分别是()[题解]令x=2，则x2=4，x221,x-2=41,x21=21,221212xxxx,由图可知选B。[例7]（2003年上海市春招试题）已知函数5)(3131xxxf，5)(3131xxxg．（1）证明f(x)是奇函数；并求f(x)的单调区间；（2）分别计算f(4)–5f(2)g(2)和f(9)–5f(3)g(3)的值，由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式，并加以证明．[题解]（1）函数f(x)的定义域为(-∞，0)∪(0，+∞)，它关于原点对称．又用心爱心专心)(55)()()(31313131xfxxxxxf，故f(x)为奇函数．设x1、x2∈(0，+∞)，且x1＜x2，)11)((5155)()(31231131231131231231131121xxxxxxxxxfxf，因312311xx＜0，31231111xx＞0，故)()(21xfxf＜0，即f(x)在（0，+∞）上单调递增．又因f(x)为奇函数，故f(x)在（-∞，0）上也是单调递增．综上，f(x)的单调（增）区间为（0，+∞），（-∞，0）．（2）计算得f(4)–5f(2)g(2)=0，f(9)–5f(3)g(3)=0．注意到2与4及3与9的平方关系，我们猜测：f(x2)–5f(x)g(x)=0，其中x≠0．下面我们给出证明．f(x2)–5f(x)g(x)=0)(51)(51555532323232313131313232xxxxxxxxxx．指数函数：函数)10(¹aaayx且叫做指数函数，其中x是自变量，函数的定义域是R。注意：为什么要规定a>0且a¹1： a<0时ax不一定有意义;a=0时，若x>0，ax=0；若x<0，则ax无意义;a=1时，y=1x=1(常量)没有研究必要.为了避免上述各种情况，所以规定a>0且a¹1...