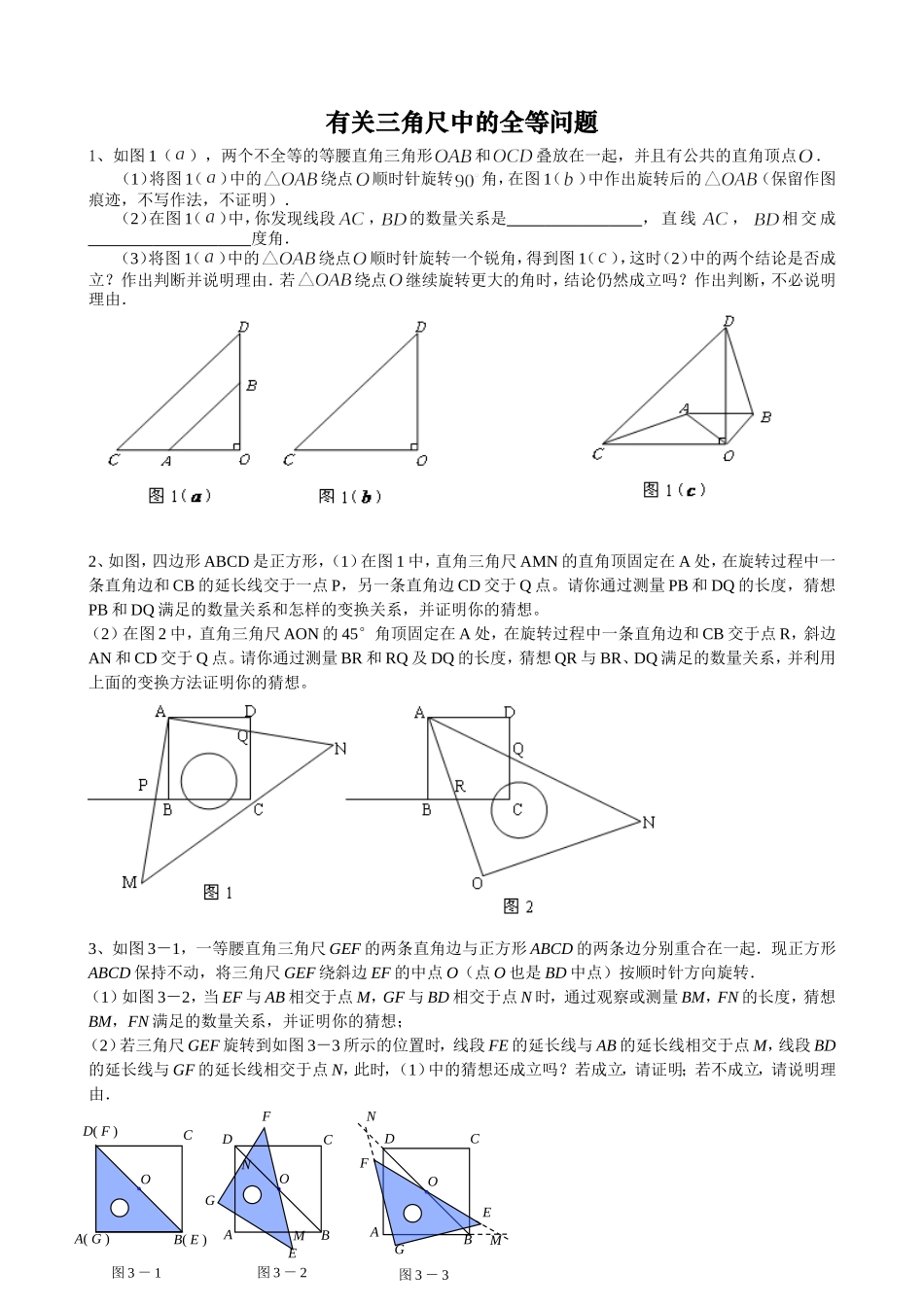
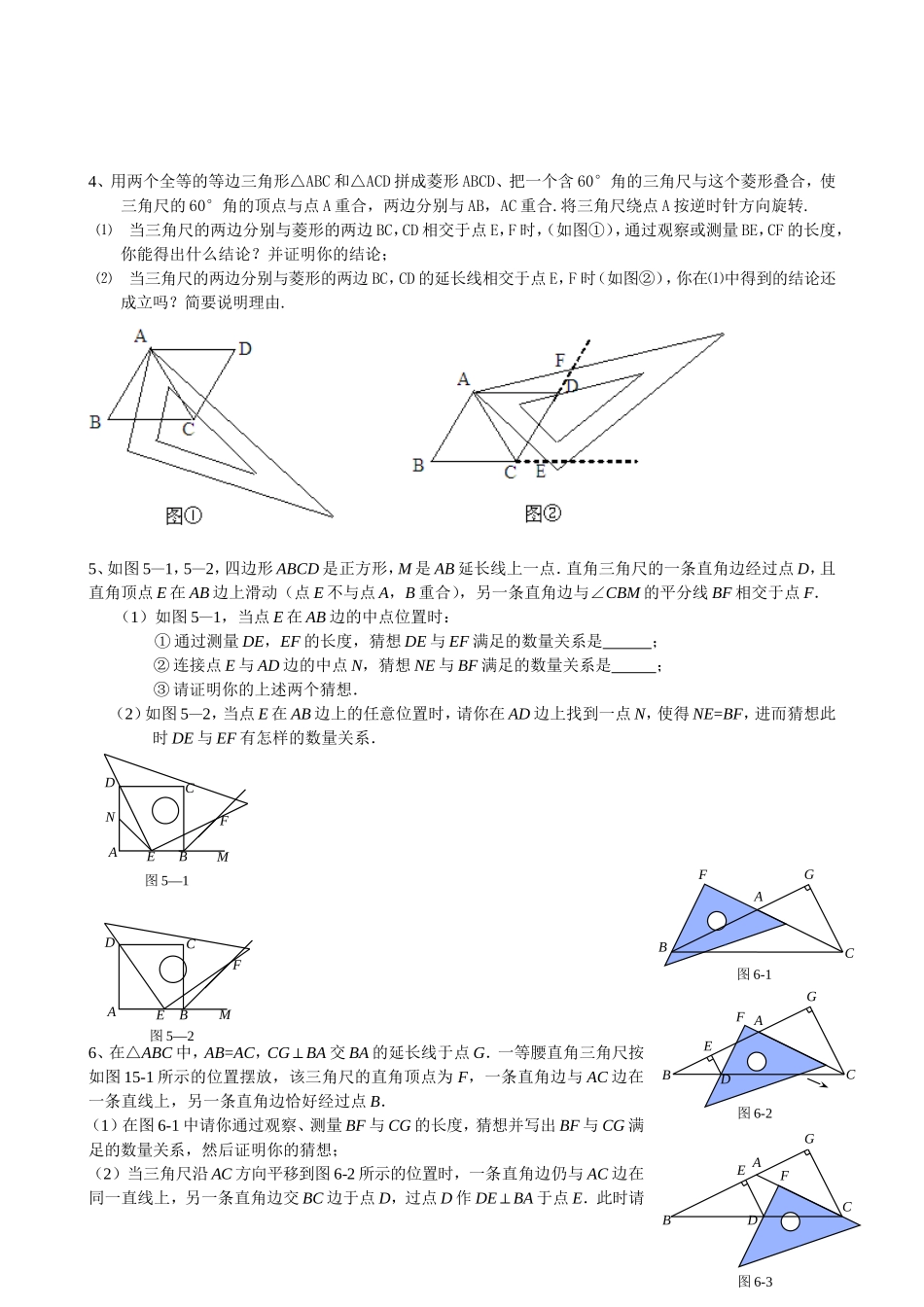
有关三角尺中的全等问题1、如图1(),两个不全等的等腰直角三角形和叠放在一起,并且有公共的直角顶点.(1)将图1()中的绕点顺时针旋转角,在图1()中作出旋转后的(保留作图痕迹,不写作法,不证明).(2)在图1()中,你发现线段,的数量关系是,直线,相交成度角.(3)将图1()中的绕点顺时针旋转一个锐角,得到图1(),这时(2)中的两个结论是否成立?作出判断并说明理由.若绕点继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.2、如图,四边形ABCD是正方形,(1)在图1中,直角三角尺AMN的直角顶固定在A处,在旋转过程中一条直角边和CB的延长线交于一点P,另一条直角边CD交于Q点。请你通过测量PB和DQ的长度,猜想PB和DQ满足的数量关系和怎样的变换关系,并证明你的猜想。(2)在图2中,直角三角尺AON的45°角顶固定在A处,在旋转过程中一条直角边和CB交于点R,斜边AN和CD交于Q点。请你通过测量BR和RQ及DQ的长度,猜想QR与BR、DQ满足的数量关系,并利用上面的变换方法证明你的猜想。3、如图3-1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.(1)如图3-2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;(2)若三角尺GEF旋转到如图3-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.图3-2EABDGFOMNC图3-1A(G)B(E)COD(F)图3-3ABDGEFOMNC4、用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD、把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.⑴当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图①),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;⑵当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图②),你在⑴中得到的结论还成立吗?简要说明理由.5、如图5—1,5—2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.(1)如图5—1,当点E在AB边的中点位置时:①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是;②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是;③请证明你的上述两个猜想.(2)如图5—2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.6、在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图15-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.(1)在图6-1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;(2)当三角尺沿AC方向平移到图6-2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请ABCDEMF图5—1NABCDEMF图5—2ABCEFG图6-2DABCDEFG图6-3ABCFG图6-1你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;(3)当三角尺在(2)的基础上沿AC方向继续平移到图6-3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)参考答案1、解:(1)如图1()(字母位置互换扣1分,无弧扣1分,不连结扣1分,扣完为止)(2);(3)成立.如图1()即:(或由旋转得)延长交于,交于(下面的证法较多),旋转更大角时,结论仍然成立.2、解:(1)①PB=DQ②DQ可以绕点A旋转90°到PB。3、解:(1)BM=FN.证明: △GEF是等腰直角三角形,四边形ABCD是正方形,∴∠ABD=∠F=45°,OB=OF.又 ∠BOM=∠FON,∴△OBM≌△OFN.∴BM=FN(2)BM=FN仍然成立.证明:...