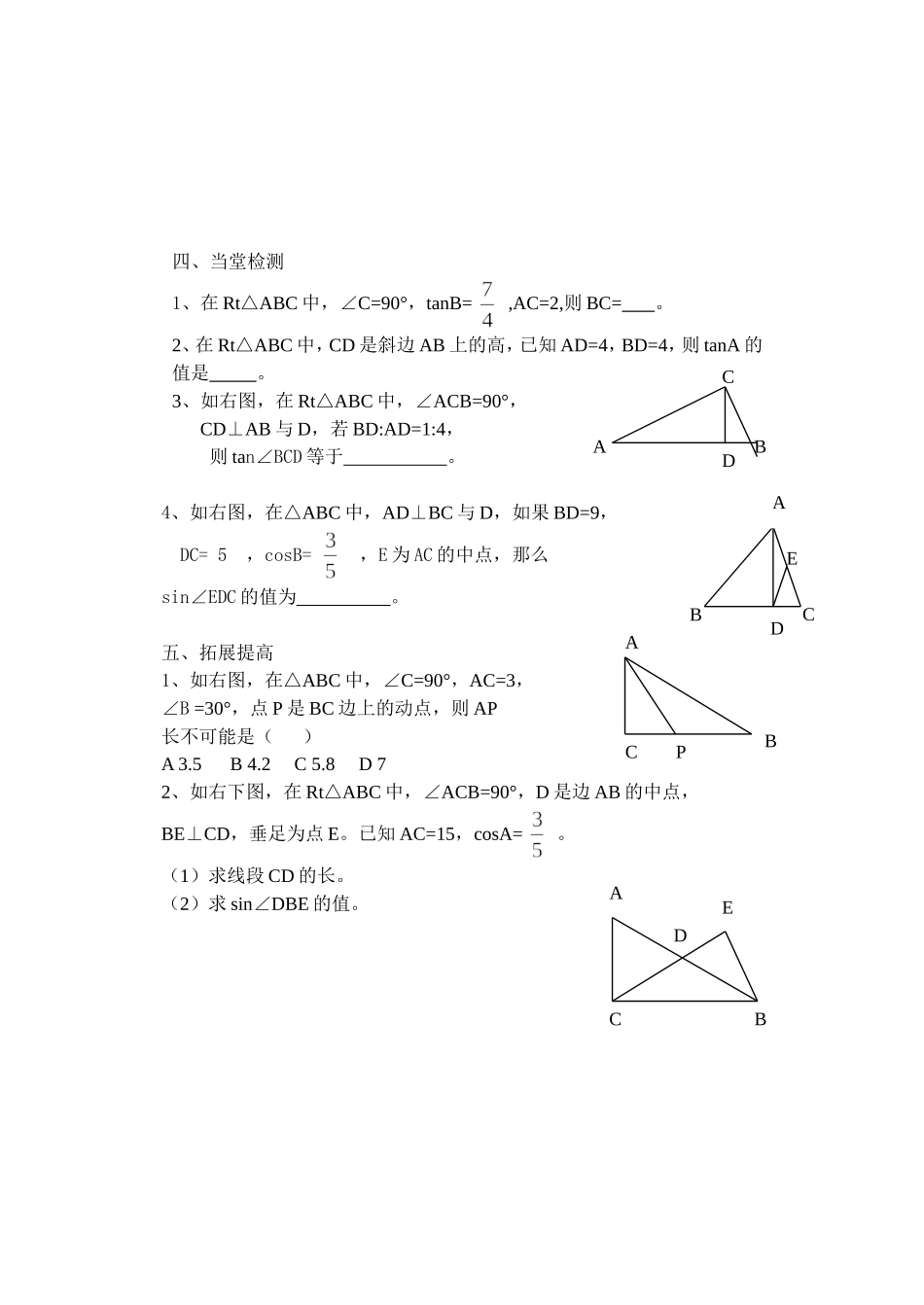
解直角三角形导学稿学习目标:1.理解解直角三角形的概念,会选择正确的解法解直角三角形。2.能综合运用直角三角形的边角关系,解决一些简单的实际问题。教学过程:一、自主学习1、直角三角形的边角关系在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,,b,,c,则直角三角形的边角关系有:(1)两锐角关系:(2)边的关系:(3)边角关系:①sinA=,a=,c=②cosA=,b=,c=.③tanA=,a=,b=.④cotA=,b=,a=2、解直角三角形由直角三角形中元素求出的过程,叫解直角三角形。在已知元素中至少要有。3、解直角三角形的两种情况(1)已知,求第三边及两锐角。(2)已知和,求其他两边及另一锐角。二、自主检测(问题反馈、组内解决)1、在锐角三角形ABC中,若,则∠C=_______。2、等边三角形的边长为a,则一边上的高为________,面积等于_______。3、在Rt△ABC中,∠C=90°,根据下列条件填空:(1)a=2,b=1,则sinA=______,(2)a=4,tanA=1.5,则b=_______(3)3a=b,则sinA=_____。三、交流展示1、在Rt△ABC中,∠ACB=90°,CD⊥AB与D,已知AC=3,AB=5,则tan∠BCD等于2、在△ABC中,∠C=90°,∠A=300,c=,解这个直角三角形。ABCD四、当堂检测1、在Rt△ABC中,∠C=90°,tanB=,AC=2,则BC=。2、在Rt△ABC中,CD是斜边AB上的高,已知AD=4,BD=4,则tanA的值是。3、如右图,在Rt△ABC中,∠ACB=90°,CD⊥AB与D,若BD:AD=1:4,则tan∠BCD等于。4、如右图,在△ABC中,AD⊥BC与D,如果BD=9,DC=5,cosB=,E为AC的中点,那么sin∠EDC的值为。五、拓展提高1、如右图,在△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是()A3.5B4.2C5.8D72、如右下图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E。已知AC=15,cosA=。(1)求线段CD的长。(2)求sin∠DBE的值。ADEBCAPABCDACBEDCB