直线和平面平行的判定VIP免费

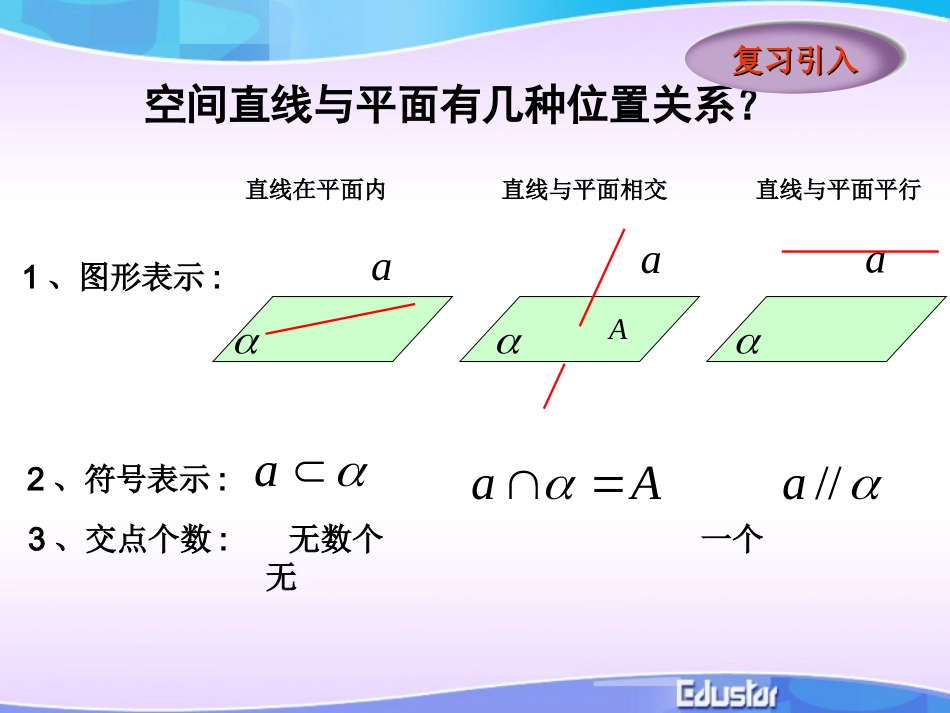
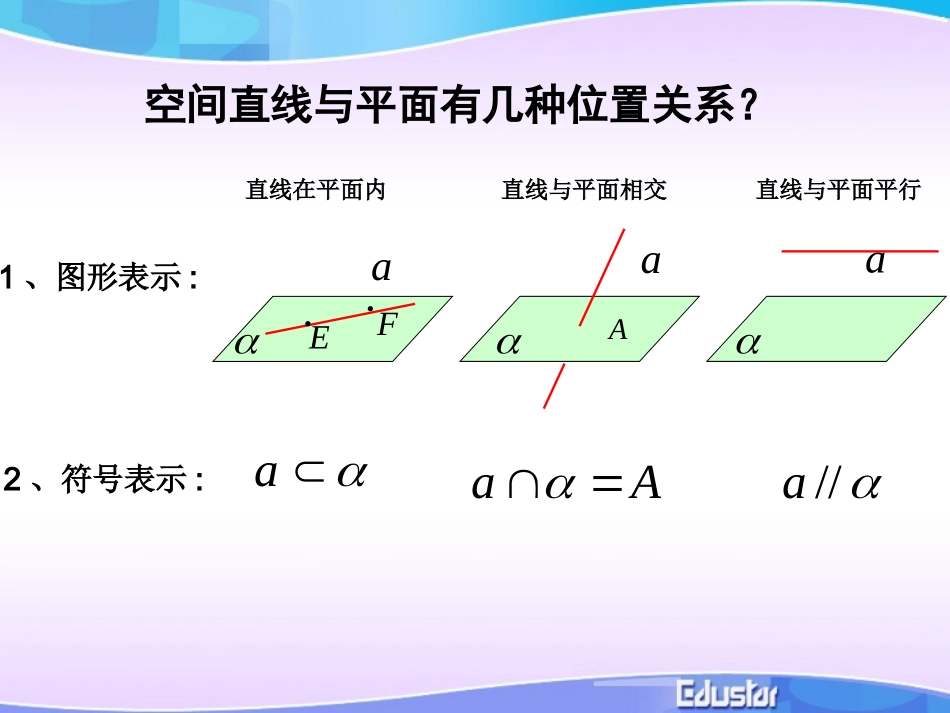
§2.2.1人教A版空间直线与平面有几种位置关系？aaa直线在平面内直线与平面相交直线与平面平行1、图形表示:2、符号表示:AaAa//a复习引入复习引入3、交点个数:无数个一个无空间直线与平面有几种位置关系？1、图形表示:2、符号表示:a直线与平面相交AAaa直线与平面平行//aa直线在平面内aEF怎样判定直线与平面平行呢？根据定义，判定直线与平面是否平行，只需判定直线与平面有没有公共点．新课开讲新课开讲但是，直线无限延长，平面无限延展，如何保证直线与平面没有公共点呢？a在生活中，注意到门扇的两边是平行的．当门扇绕着一边转动时，另一边始终与门框所在的平面没有公共点，此时门扇转动的一边与门框所在的平面给人以平行的印象．实例感受实例感受ABDC在门扇的旋转过程中:直线AB在门框所在的平面外直线CD在门框所在的平面内直线AB与CD始终是平行的将一本书平放在桌面上，翻动书的封面，封面边缘AB所在直线与桌面所在平面具有什么样的位置关系？DCAB在封面翻动过程中:直线AB在桌面所在的平面外直线CD在桌面所在的平面内直线AB与CD始终是平行的ba如果平面内有直线与直线平行，那么直线与平面的位置关系如何？aba是否可以保证直线与平面平行？a（1）这两条直线共面吗？（2）直线与平面相交吗？a不相交ab共面.ba内的直线平行于平面外有一条直线平面抽象概括直线与平面平行的判定定理：若平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.简述为：线线平行线面平行直线与直线平行关系直线与平面间平行关系平面问题空间问题ab////,,abababa思辨论证思辨论证.////,,ababa，求证：已知证明：.不平行于平面假设a.,PPaPaa，则，相交，设交点为与平面.//bPbaPcabcP，有作直线过//.//a假设错误，则cacbba//.////，.矛盾这与PcaabcP面证明有一定的难度，线面平行的判定定理正反面入手“正难则反”，不妨从反证法思辨论证思辨论证αβbpcbα////,,ababa，求证：已知证法二：.不平行于平面假设a.,PPaPaa，则，相交，设交点为与平面..bPbPb或则又.//矛盾这与，，则若baAbabP矛盾。异面，也与、，则若bababP//.//a则综上所述，假设错误，aa反设归谬判断注意：1、在反设过程中注意思维的严密性，2、贯彻分类讨论思想，对可能出现的各种情况进行讨论。（1）定义法：证明直线与平面无公共点；（2）判定定理：证明平面外直线与平面内直线平行．怎样判定直线与平面平行？////ababa例1、如图，长方体中，DCBAABCDAABBCCDD（1）与平行的平面是；（2）与平行的平面是；（3）与平行的平面是；平面DCBADDCC平面DDCC平面平面CBCB平面DCBA平面CBCBAB'AAAD脱口而出脱口而出思考交流思考交流如图，正方体如图，正方体中，中，是棱的中点，过点是棱的中点，过点画一条直线使之与截面平行画一条直线使之与截面平行..1111ABCDABCD11AB11ABCDPPPQABCD1B1C1A1DM分析：EF在面BCD外，要证明EF∥面BCD，只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢？典例赏析典例赏析AEFBDCBDEF//根据中位线定理的中点，、分别为、中，在证明：如图，连接ADABFEABDBD.,,ABDBDABDEF平面平面又ABDEF平面//解后反思：通过本题的解答，你可以总结出什么解题思想和方法？.//.BCDEFADABFEABCD平面求证：的中点与分别是、中，如图，空间四边形例1、要证明直线与平面平行可以运用判定定理；线线平行线面平行能够运用定理的条件是要满足三点，“面外、面内、平行”。运用定理的关键是找平行线。找平行线又经常会用到三角形中位线定理。反思1：反思2：反思3：////aabba解：连接BD交AC于点O,连接OE,在DDB中，E，O分别是BDDD,的中点．DBEO//ACEEO平面ACEBD平面'AECBD平面//'变式训练变式训练..''''''由的位置关系，并说明理与平面试判断的中点是中，...