矢量场的环量及旋度VIP免费

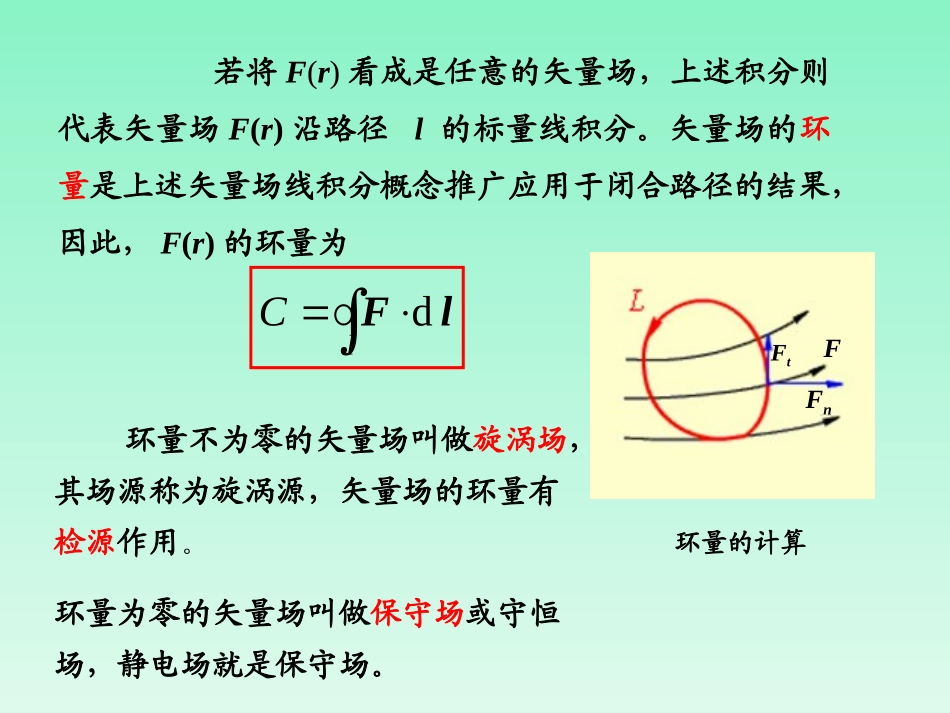
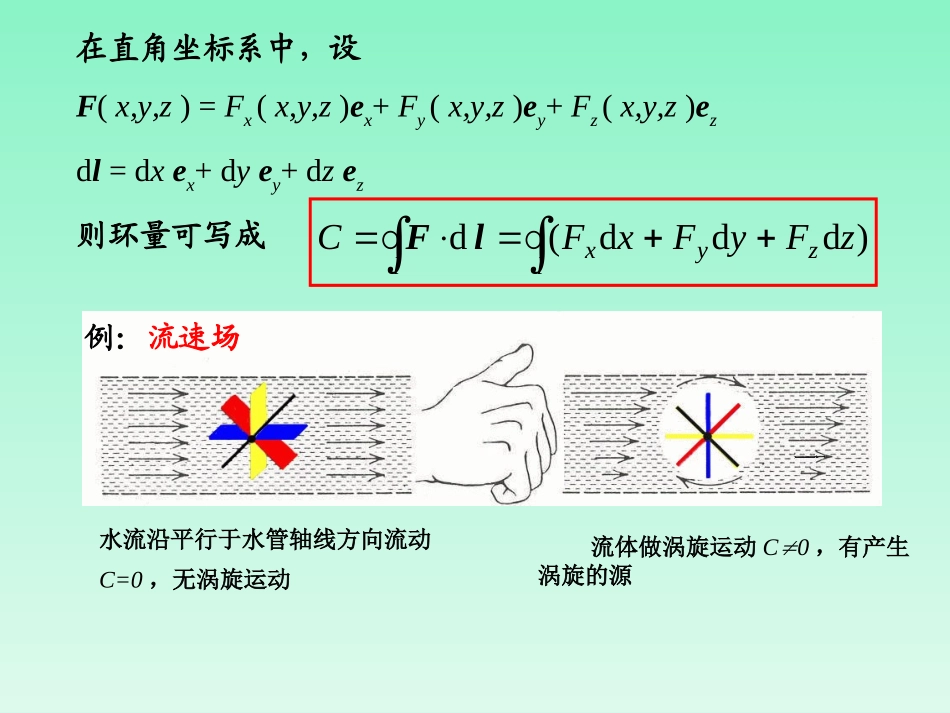
§1.4矢量场的环量及旋度1、环量矢量场沿闭合线的线积分从变力作功问题引入矢量场环量的概念。iiiiiilFAlFcoslNiiilNAldF)lF(lim10一段积分路径及其细分θiΔliFiba‘‘‘‘‘‘‘l若将F(r)看成是任意的矢量场，上述积分则代表矢量场F(r)沿路径l的标量线积分。矢量场的环量是上述矢量场线积分概念推广应用于闭合路径的结果，因此，F(r)的环量为环量不为零的矢量场叫做旋涡场，其场源称为旋涡源，矢量场的环量有检源作用。环量为零的矢量场叫做保守场或守恒场，静电场就是保守场。lClFdFnFtF环量的计算水流沿平行于水管轴线方向流动C=0，无涡旋运动流体做涡旋运动C0，有产生涡旋的源例：流速场在直角坐标系中，设F(x,y,z)=Fx(x,y,z)ex+Fy(x,y,z)ey+Fz(x,y,z)ezdl=dxex+dyey+dzez则环量可写成lzyxlzFyFxFC)ddd(dlF过点P作一微小有向曲面S,它的边界曲线记为l,曲面的法线方向与曲线绕向成右手螺旋关系。当S点P时,存在极限SSClSlFdlimdd0上式称为环量密度过点P的有向曲面S取不同的方向，其环量密度将会不同。2、旋度（1）环量密度面元法向矢量与周界循行方向的右手关系。PlSne（2）旋度nlsscurlelFFmax0dlimP点的旋度定义为该点的最大的环量密度，并令其方向为en,即旋度与环量密度的关系：投影scurlcurllsnnlFeFFdlim)(0zzyxFyzzyxFzzyyxFyzyxFzyzyl)()()()(d,,,,,,,,lFzFyFScurlyzxlSxxlFFdlim)(0旋度直角坐标式的推导于是得旋度的x方向分量：Fzl1xyzΔsx(x,y,z)ΔyΔzFyFz(x,y+Δy,z)Fy(x,y,z+Δz)o推导旋度的直角坐标式所取的面元和它的围线zzyxFyzzzyxFzyxFzyyzyxFzyxFyzyxFzyyzzy)()()()()()(,,,,,,,,,,,,xyzyzSzFyFzyzFyF)()(同理可求得curlF的y，z分量yFxFcurlxFzFcurlxyzzxy)(,)(FF所以zxyyzxxyzyFxFxFzFzFyFcurleeeF)()()(zyxzyxFFFzyxeeeF或用算符将其写成(3）旋度的物理意义•矢量的旋度仍为矢量，是空间坐标点的函数。•点P的旋度的大小是该点环量密度的最大值。•在矢量场中，若F=J0,称之为旋度场(或涡旋场)，J称为旋度源密度(或涡旋源密度)；•点P的旋度的方向是该点最大环量密度的方向。•若矢量场处处F=0，称之为无旋场或保守场。(4）有关旋度的几个关系式•相对位置矢量的旋度为零，即0R•f(r)与F(r)之积fF的旋度有恒等式FFFfff)()(0R)(Rf•f(R)与R之积的旋度，有证明：0RRddRdd0R)(R)(R)(RRfRRfRfRfRf0r例4已知F=(2xyz)ex(x+yz2)ey+(3x2y+4z)ez试就图所示xoy平面上以原点为心、3为半径的圆形路径，求F沿其逆时针方向的环量。解在xoy平面上，有F=(2xy)ex+(x+y)ey+(3x2y)ez，dl=dxex+dyeyllyyxxyxdd2dlF设x=3cos，y=3sinπ18sin219dcossin19dcossin9cossin9dcos3sin3cos3d3sinsin3cos32dπ2022π02π022π20llF则xy(x,y)l3o例5求矢量场F=xyz（exey+ez)在点M(1,3,2)处的旋度。解：zyxzyxzyxzyxxzyzyzxyxyxzxyzyxyzxxyzxxyzzxyzzxyzyFFFzyxeeeeeeeeeFzyxzyxeeeeeeF43266332M作业：1.8