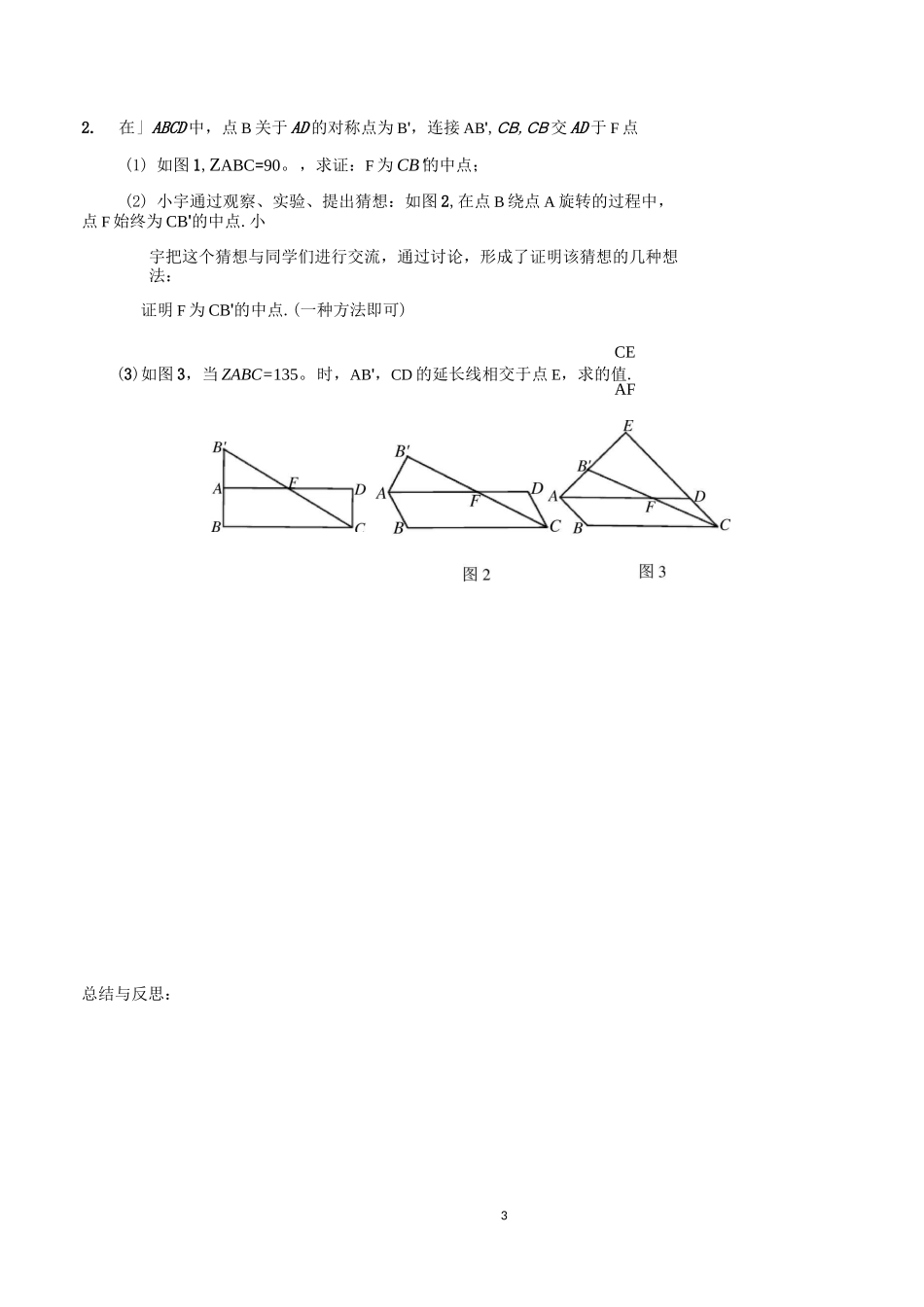
1有关中点的专题基本知识方法储备:1.线段垂直平分线的性质:2.三角形中线把三角形分成面积相等的两个三角形中点的应用:1.倍长构造全等(构造平行四边形)3.找另一边的中点出中位线(或过点M做三角形一边平行线出中点,进而出中位线)4.直角三角形中斜边中线等于斜边一半5.-----------------------------圆中:过圆心和弦的中点'A过圆心和弦所对弧的中点*弦的垂直平分线1二与中点有关的思路:•斜边中线(中点+直角);中位线(中点+中点);倍长(8字全等);垂直平分线;2.过线段一个端点作中线的平行线出中位线21•在正方形ABCD中,点P是射线CB上一个动点,连接PA,PD,点M,N分别为BC,AP的中点,连接MN交PD于点Q.(1)如图1,当点P与点B重合时,VQPM的形状是.(2)当点P在线段CB的延长线上时,如图2.①依题意补全图2;②判断VQPM的形状,并加以证明;图1图2总结与反思:32.在」ABCD中,点B关于AD的对称点为B',连接AB',CB,CB交AD于F点(1)如图1,ZABC=90。,求证:F为CB'的中点;(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB'的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:证明F为CB'的中点.(一种方法即可)CE(3)如图3,当ZABC=135。时,AB',CD的延长线相交于点E,求的值.AF总结与反思:43.在△ABC中,AB=BC,BD丄AC于点D.(1)如图1,当ZABC=90°时,若CE平分ZACB,交AB于点E,交BD于点F.①求证:ABEF是等腰三角形;②求证:BD=-(BC+BF);2(2)点E在AB边上,连接CE.若BD=2(BC+BE),在图2中补全图形,判断ZACE与ZABC之间的数厶量关系,写出你的结论,并写出求解ZACE与ZABC关系的思路.图1图2总结与反思:54.四边形ABCD是正方形,NBEF是等腰直角三角形,ZBEF=90。,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC。EC(1)如图24-1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及--的值;GC(2)将图24-1中的ABEF绕点B顺时针旋转至图24-2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图24-1中的ABEF绕点B顺时针旋转«(0°<«<90。),若BE=1,AB二迈,当E,F,D三点共线时,求DF的长及tanZABF的值。总结与反思:图24-DC备用6在矩形ABCD中,将对角线CA绕点C逆时针旋转得到CE,连接AE,取AE的中点F,连接BF,DF.()若点E在CB的延长线上,如图1①依题意补全图1;②判断BF与DF的位置关系并加以证明;()若点E在线段BC的下方,如果ZACE=90°,ZACB=28°,AC=6,请写出求BF长的思路(可以不写出计算结果)°°图备用图总结与反思:在RtAABC中,斜边AC的中点M关于BC的对称点为点O,将△ABC绕点O顺时针旋转至ADCE,连接BD,BE,如图所示.(1)________________________________________________________在①ZBOE,②ZACD,③ZCOE中,等于旋转角的是(填出满足条件的的角的序号);(2)若ZA=Q,求/BEC的大小(用含a的式子表示);(3)点N是BD的中点,连接MN,用等式表示线段MN与BE之间的数量关系,并证明.总结与反思:O