匀变速直线运动的位移与时间的关系 (2)VIP免费

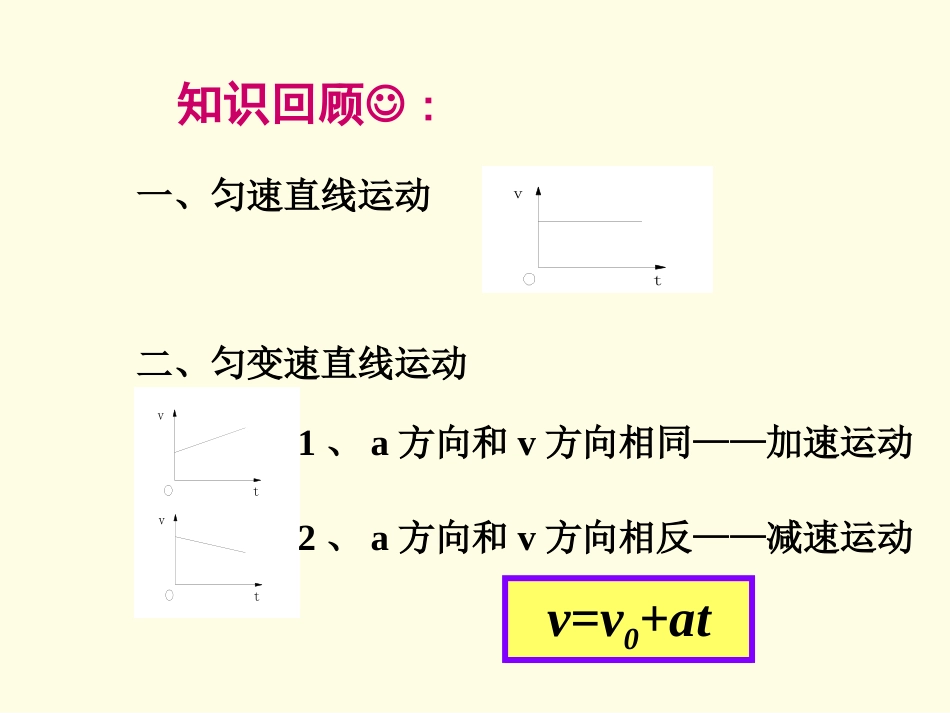
知识回顾:vt一、匀速直线运动二、匀变速直线运动tvtv1、a方向和v方向相同——加速运动2、a方向和v方向相反——减速运动v=v0+at2.3匀变速直线运动的位移与时间的关系一、匀速直线运动的位移问题1：匀速直线运动的位移公式？在时间t内的位移：x=vt问题2：在v-t图象中如何表示位移？对于匀速直线运动，物体的位移对应着v-t图象中一块矩形的面积猜想与假设：对于匀变速直线运动，物体的位移是否也对应着v-t图象下面的“面积”？v0vott思考与讨论下面是某一物体在下面是某一物体在0~0.5s0~0.5s内做匀加内做匀加速直线运动的情况（见下表），表中“速度”速直线运动的情况（见下表），表中“速度”一行是物体在一行是物体在00、、11、、22…………55几个位置的瞬几个位置的瞬时速度时速度。。位置编号012345时间t/s00.10.20.30.40.5速度(m/s)0.40.60.81.01.21.4能不能根据表中的数据，用最简便的方法估算这一物体在0到0.5s内的位移？回顾与提示：瞬时速度可以用“某一小段时间内的平均速度粗略地表示。反其道：是否可以用某一时刻的瞬时速度来代表这一时刻附近的、一小段时间的平均速度呢？位置编号012345时间t/s00.10.20.30.40.5速度(m/s)0.40.60.81.01.21.4览于上述推理：是否可以认为0~0.1s内的平均速度近似等于0.4m/s,0.1~0.2s内的平均速度近似等于0.6m/s,0.1~0.2s内的平均速度近似等于0.8m/s,……思考：0~0.5s内的位移可否近似估算为：x＝0.4×0.1＋0.6×0.1＋0.8×0.1＋1.2×0.1＋1.4×0.1＝……上述方法的思想是把物体在0~0.1s内看作是速度为0.4m/s的一段匀速运动；0.1~0.2s内看作是速度为0.6m/s的一段匀速运动；0.1~0.2s内看作是速度为0.8m/s的一段匀速运动,……然后多个小段匀速运动的位移之和为0~0.5s内位移。vt00.40.10.20.30.5在图象上的几何特征是什么样子呢？思考：1）如果要提高估算的精确程度，有什么更好的方法吗？2）如果当初实验时的时间间隔不是取0.1s，而是取得更小些，比如0.02s，同样用这个方法计算，误差是不是会小一些？3）如果取0.002s、0.0002s……误差又会怎样？误差是不是会小一些？从v-t图象中探究匀变速直线运动的位移1234梯形OABC的面积就代表做匀变速直线运动物体在0（此时速度为v0）到t（此时速度为v）这段时间的位移。V1V2V3V4V0VV0ttt1t2t3t4结论：在匀变速直线运动的结论：在匀变速直线运动的v-tv-t图象中，物体图象中，物体的位移的位移xx在数值上等于图线与坐标轴所围的面在数值上等于图线与坐标轴所围的面积。积。（横轴上方的面积与横轴下方的面积有什么分别（横轴上方的面积与横轴下方的面积有什么分别？）？）分割和逼近的方法在物理学研究中有着广泛的应用。早在公元263年，魏晋时的数学家刘徽首创了“割圆术”——圆内正多边形的边数越多，其周长和面积就越接近圆的周长和面积。割圆术割圆术VV0t二、匀变速直线运动的位移公式由图可知：梯形OABC的面积S=（OC+AB）×OA/2代入各物理量得：tvvx)(210又v=v0+at得：2021attvx1、从v-t图象推导：aatt1122——22tv0△vxx==vv00tt++atat1122——22vv00ttvv0ttv0tv0△vvv0ttv0vv00ttaatt1122——22二.匀变速直线运动的位移1.位移公式：221t0vatx2.对位移公式的理解:⑴反映了位移随时间的变化规律。⑵因为υ0、α、x均为矢量，使用公式时应先规定正方向。（一般以υ0的方向为正方向）若物体做匀加速运动,a取正值,若物体做匀减速运动,则a取负值.(3)若v0=0,则x=212at(4)特别提醒:t是指物体运动的实际时间,要将位移与发生这段位移的时间对应起来.(5)代入数据时,各物理量的单位要统一.(用国际单位制中的主单位)例1.一质点以一定初速度沿竖直方向抛出，得到它的速度一时间图象如图2—3—6所示．试求出它在前2s内的位移，后2s内的位移，前4s内的位移．5m-5m0例2：一辆汽车以1m/s2的加速度行驶了12s，驶过了180m。汽车开始加速时的速度是多少？解：以汽车运动的初速v0为正方向由得：2021attvxsmsmattxv/9/12121121802101、解:以汽车初速度方向为正方向2021attvx所以由得：车的位移：例3、在平直公路上，一汽车的速度为15m/s。从某时刻开始刹车，在阻力作用下，汽车以2m...