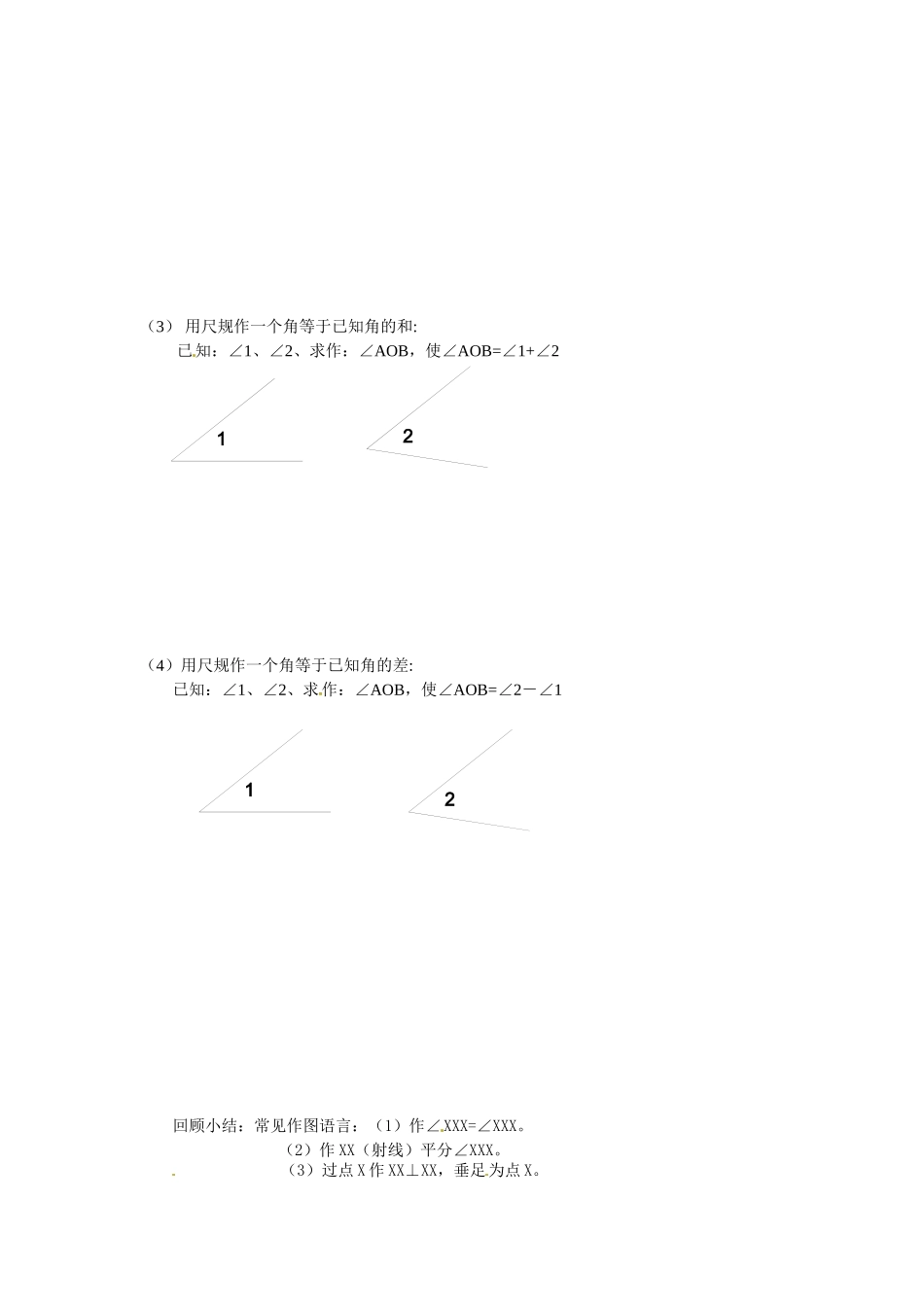
2.4用尺规作角一、学习目标:1、会用尺规作一个角等于已知角。二、学习重点:1、作一个角等于已知角。2、作角的和、差、倍数等。三、学习难点:作角的和、差、倍。四、学习设计(一)预习准备(1)预习课本55-56页(2)思考①什么叫尺规作图?②直尺的功能?圆规的功能?(3)预习作业利用尺规按下列要求作图(1)延长线段BA至C,使AC=2ABBA(2)延长线段EF至G,使EG=3EFFE(3)反向延长MN至P,使MP=2MNNM(二)学习过程1、(1)只用没有的直尺和作图成为尺规作图。(2)尺规作图时,直尺的功能是(1),(2)圆规的功能是(1),(2)[来源:学#科#网]例1下列说法正确的是()A、在直线l上取线段AB=aB、做,使得C、延长射线OAD、反向延长射线OB例2作图(1)用尺规作一个角等于已知角.已知:∠。求作:∠AOB,使∠AOB=∠[来源:学科网](2)用尺规作一个角等于已知角的倍数:已知:∠1求作:∠MON,使∠MON=2∠1[来源:Zxxk.Com]1(3)用尺规作一个角等于已知角的和:已知:∠1、∠2、求作:∠AOB,使∠AOB=∠1+∠2(4)用尺规作一个角等于已知角的差:已知:∠1、∠2、求作:∠AOB,使∠AOB=∠2-∠1[来源:Zxxk.Com][来源:学|科|网]回顾小结:常见作图语言:(1)作∠XXX=∠XXX。(2)作XX(射线)平分∠XXX。(3)过点X作XX⊥XX,垂足为点X。1212第二章平行线与相交线2.1两条直线的位置关系一、学习目标:1、知识目标:在具体情景中了解对顶角、补角、余角,知道对顶角相等、等角的余角相等、等角的补角相等,并能解决一些实际问题。2、能力目标:(1)经历观察、操作、推理、交流等过程,发展空间观念、推理能力和有条理地表达的能力。(2)能运用互为余角、互为补角、对顶角等相关的知识解决一些实际问题。3、情感目标:在活动中培养学生乐于探究、合作的习惯,体验探索成功、感受创新的乐趣,从而培养学习数学的主动性;进一步体会“数学就在我们身边”,增强学生用数学解决实际问题的意识。二、学习重点:了解补角、余角、对顶角,知道等角的余角相等、等角的补角相等、对顶角相等。三、学习难点:学生探索等角的余角相等、等角的补角相等、对顶角相等的过程以及对其意义的理解,并能解决一些实际问题。初步的“说理”也是难点之一。四、学习设计:(一)预习准备(1)预习书38、39页(2)回顾:①什么是直角?②什么是平角?(3)预习作业:①在一副三角板中,每块都有一个角是90°,那么其余两个角的和是多少?②已知∠1=36°,∠2=54°,那么∠1+∠2=_________③已知∠1=144°,∠2=36°,那么∠1+∠2=_________(二)学习过程:1、创设情境,引入课题⑴请同学们拿出事先准备好的直角纸板,用剪刀把直角从顶点剪开,问:这两个角有什么关系?⑵再拿出平角纸板并用剪刀把平角从顶点剪开,问:这两个角有什么关系?⑶请同学们分别给这两个角命名——引入课题2、展示新知:⑴在一副三角尺中,每块都有一个角是90o,而其他两个角的和是90o。一般情况下,如果两个角的和等于90o(直角),我们就说这两个角互为余角,即其中一个角是另一个角的余角.例如,∠1与∠2互为余角,∠1是∠2的余角,∠2也是∠1的余角.同样,如果两个角的和等于180o(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.⑵符号语言:若∠1+∠2=90o,那么∠1与∠2互余。12999.com2113∠与∠42若∠3+∠4=180o,那么∠3与∠4互补。3、注:(1)“互为”这个词语,与“互为相反数”、“互为倒数”等词语中的含义有联系,均表示成对出现;(2)互为余角以及互为补角的角,主要反映了角的数量关系,而不是角的位置关系,可以把剪下的∠1、∠2、∠3、∠4摆放出各种不同位置。(3)区分互为补角和互为余角,区别在于两角的和是180°还是90°。[来源:学科网ZXXK]4、应用新知体验成功⑴若∠1与∠2互余,则∠1+∠2=__________⑵若∠1=90o—∠2,则∠1+∠2=__________⑶60O32’的补角是_______,余角是_______(一个角的余角一定比这个角的补角小吗?)⑷30O角的余角的补角是__________⑸填表:[来源:Zxxk.Com][来源:学#科#网Z#X#X#K]⑹若一个角是它余角的4倍,求这个角。变式训练:(1)一...