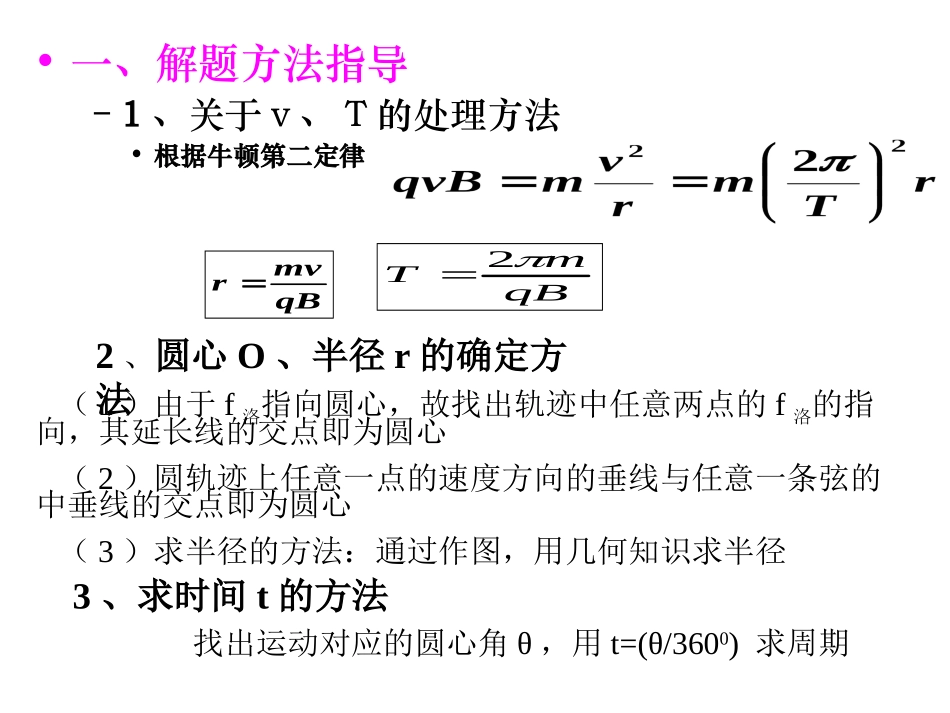
带电粒子在磁场中做匀速圆周运动带电粒子在磁场中做匀速圆周运动习题课习题课知识回顾•1、带电粒子垂直进入匀强磁场受到的洛仑兹力f=———•2、带电粒子垂直进入磁场做圆周运动的向心力由什么来提供?其轨道半径r和周期T如何计算?qvB•一、解题方法指导–1、关于v、T的处理方法•根据牛顿第二定律qBmvrqBmT22、圆心O、半径r的确定方法(1)由于f洛指向圆心,故找出轨迹中任意两点的f洛的指向,其延长线的交点即为圆心(2)圆轨迹上任意一点的速度方向的垂线与任意一条弦的中垂线的交点即为圆心(3)求半径的方法:通过作图,用几何知识求半径3、求时间t的方法找出运动对应的圆心角θ,用t=(θ/3600)求周期②已知粒子的入射点和出射点的位置时,可以通过入射点作入射方向的垂线,再连接入射点和出射点作其中垂线,这两条垂线的交点就是圆弧轨道的圆心,如图乙所示,P为入射点,图3-6-1M为出射点,这种方法在不明确出射方向的时候使用。③若仅知道粒子进入磁场前与离开磁场后的速度方向,可找两速度方向延长线夹角的角平分线以确定圆心位置范围,再结合其他条件以确定圆心的具体位置。•二、例题讲解•〖例1〗如图所示,一束电子(电量为e)以速度V垂直射入磁感应强度为B宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角300。求:(1)电子的质量m=?(2)电子在磁场中的运动时间t=?dBeθvOθ【分析】过入射点和出射点粗略画出电子的轨迹作入射点和出射点的速度垂线交于一点O即为圆心过出射点作磁场左边界的垂线由几何知识求半径:r=d/sinθ结合牛顿第二定律qvB=mv2/r得m=2deB/v电子在磁场中的运动时间为t=(θ/3600)T=(1/3)(2m/qB)=d/3v–二、例题讲解–〖例2〗长为L的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁场强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力),从左边极板间中点处垂直磁场以速度v平行极板射入磁场,欲使粒子不打在极板上,则粒子入射速度v应满足什么条件?+qmvLLB•〖例3〗X轴上方有场强为E的匀强电场,x轴下方有匀强磁场B,方向如图所示。在X轴上有一点C,离O点的距离L,现有一带正电的离子+q在y轴上的A点由静止释放后,恰好经过C点。问A点的坐标应满足什么条件?【解答】离子从A点释放后,在电场力的作用下加速运动,然后以一定的速度V进入磁场,在洛仑兹力作用下做半个圆运动,又进入电场做减速运动,速度减为零后又加速运动。。。。。。,如此往复。yOCAx+qEBLy要使离子经过C点,O、C的距离应等于离子圆运动轨迹直径的整数倍,即L=n(2r)(n=1、2、3…)①设离子进入磁场的速度V,由牛顿第二定律qvB=mv2/r②在电场中,根据动能定理qEy=mv2/2③联立①②③得y=qB2L2/(8n2mE)(n=1、2、3…)课堂训练•1.如图所示,以O点为圆心、半径R为的圆形真空内,有垂直纸面的匀强磁场。一带电离子从A点正对O点以V的速度射入磁场中,从C点射出磁场