圆的参数方程VIP免费

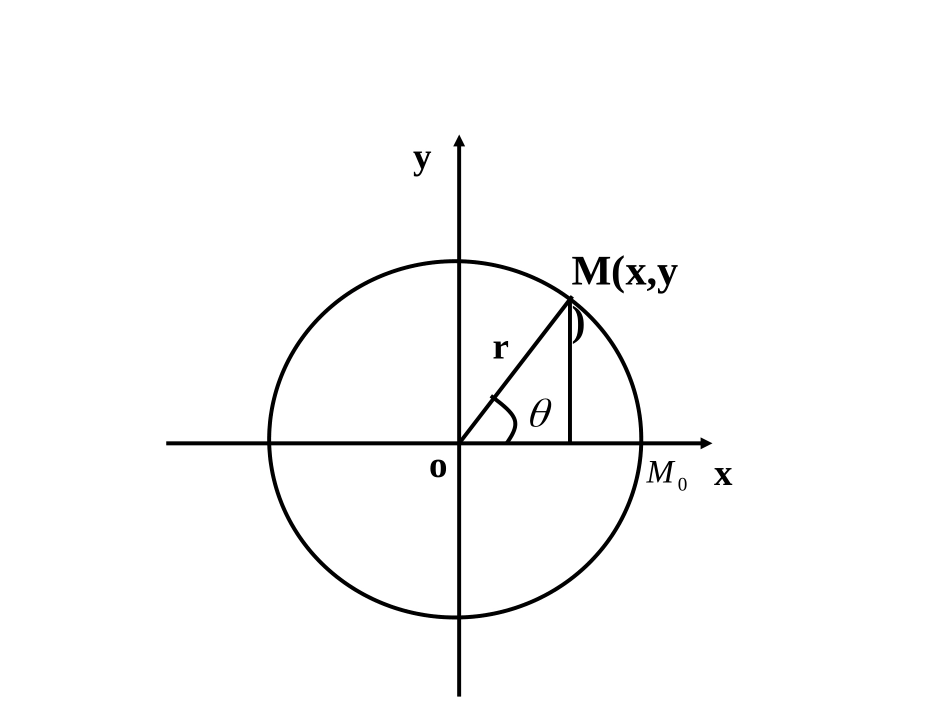
2、圆的参数方程yxorM(x,y)0M)()(sincos{sin,cos),(速圆周运动的时刻质点作匀有明确的物理意义程。其中参数的圆的参数方，半径为这就是圆心在原点为参数即角函数的定义有：，那么由三＝，设＝，那么，坐标是转过的角度是，点如果在时刻trOttrytrxrytrxtrOMtyxMMt转过的角度。的位置时，到逆时针旋转绕点的几何意义是其中参数的圆的参数方程，半径为这也是圆心在原点为参数为参数，于是有，也可以取＝考虑到00)(sincos{OMOMOOMrOryrxt圆的参数方程的一般形式么样的呢？的圆的参数方程又是怎半径为那么，圆心在点普通方程是的参数方程，它对应的以上是圆心在原点的圆ryxoryx),(,002222220000cos{()s()()inxxyxxryyyrr对应的普通方程为为参数由于选取的参数不同，圆有不同的参数方程，一般地，同一条曲线，可以选取不同的变数为参数，因此得到的参数方程也可以有不同的形式，形式不同的参数方程，它们表示的曲线可以是相同的，另外，在建立曲线的参数参数时，要注明参数及参数的取值范围。例、已知圆方程x2+y2+2x-6y+9=0，将它化为参数方程。解：x2+y2+2x-6y+9=0化为标准方程，（x+1）2+（y-3）2=1，∴参数方程为sin3cos1yx(θ为参数)例2如图，圆O的半径为2，P是圆上的动点，Q(6,0)是x轴上的定点，M是PQ的中点，当点P绕O作匀速圆周运动时，求点M的轨迹的参数方程。yoxPMQ)(sin3cos{sin2sin2,3cos26cos2),sin2,cos2(,),(为参数的轨迹的参数方程是所以，点由中点坐标公式得：的坐标是则点，的坐标是解：设点yxMyxPxOPyxMyoxPMQ0022000022000022(,),(,)4{26226,2,4(3)1MxyPxyxyxxyyxxyyxyMxy另解：设那么将代入，可得点的轨迹方程是yoxPMQ径，并化为普通方程。表示圆的圆心坐标、半所为参数、指出参数方程)(sin235cos2{2yx4)3()5(22yx_____________4)0(sin2cos{3，则圆心坐标是是的直径为参数，、圆rrryrrx（2，1）