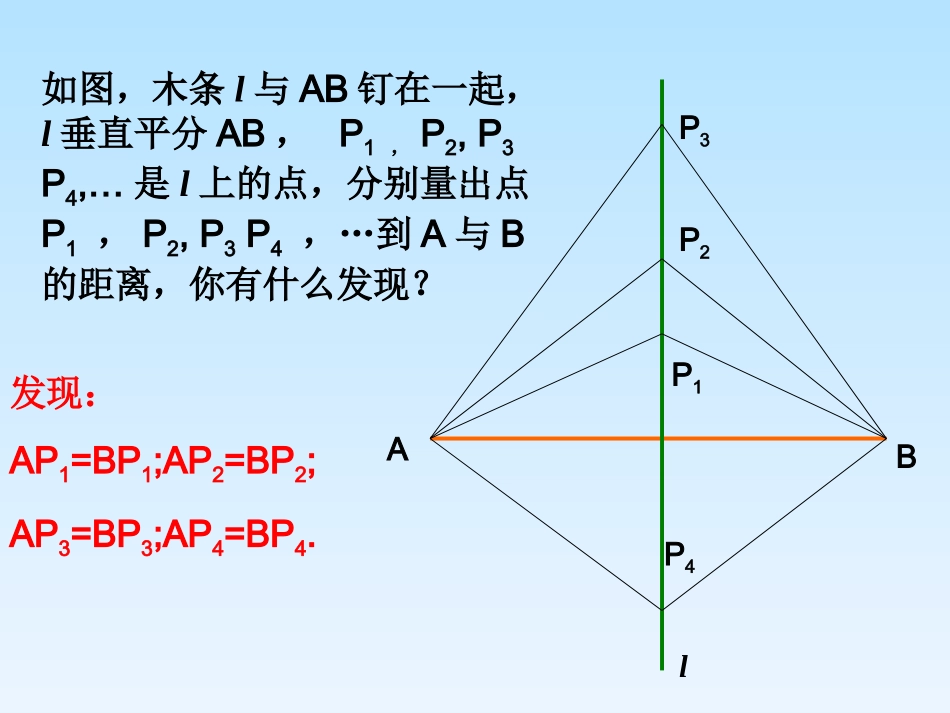
ABlP1P2P3P4如图,木条l与AB钉在一起,l垂直平分AB,P1,P2,P3P4,…是l上的点,分别量出点P1,P2,P3P4,…到A与B的距离,你有什么发现?发现:AP1=BP1;AP2=BP2;AP3=BP3;AP4=BP4.动动手,你也会有发现!动动手,你也会有发现!画画线段线段ABAB的垂直平分线的垂直平分线ll,在,在ll上取任意点上取任意点PP,,量量一量点一量点PP到到AA与与BB的的距离距离,你有什么,你有什么发现发现?再取几个?再取几个点试试。你能点试试。你能说明说明理由吗?理由吗?结论:结论:线段垂直平分线上的点与这条线段两个线段垂直平分线上的点与这条线段两个端点的距离相等端点的距离相等..已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在l上.求证:PA=PB.探索并证明线段垂直平分线的性质求证:“线段垂直平分线上的点到线段两端点的距离相等.”ABPClABCPl已知:直线lAB⊥,垂足是C,AC=CB,点P在l上。求证PA=PB.证明: lAB⊥,∴∠PCA=PCB=90°∠又 AC=CB,PC=PC,∴△PCAPCB(SAS)≌△∴PA=PB线段垂直平分线上的点与这条线段两个端点的距离相等。线段垂直平分线的性质:PAlCB几何语言: l⊥ABAC=BC∴PA=PB8课堂练习练习1如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于______.ABCDE解: AD⊥BC,BD=DC,∴AD是BC的垂直平分线,∴AB=AC. 点C在AE的垂直平分线上,∴AC=CE.∴AB=AC=CE. AB=CE,BD=DC,∴AB+BD=CD+CE.即AB+BD=DE.课堂练习练习2如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?ABCDE探索并证明线段垂直平分线的判定反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?点P在线段AB的垂直平分线上.已知:如图,PA=PB.求证:点P在线段AB的垂直平分线上.PABC探索并证明线段垂直平分线的判定证明:过点P作线段AB的垂线PC,垂足为C.则∠PCA=∠PCB=90°.在Rt△PCA和Rt△PCB中, PA=PB,PC=PC,∴Rt△PCA≌Rt△PCB(HL).∴AC=BC.又PC⊥AB,∴点P在线段AB的垂直平分线上.PABC已知:如图,PA=PB.求证:点P在线段AB的垂直平分线上.与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。线段垂直平分线的判定:PAlCB几何语言: PA=PB∴P是AB的垂直平分线上的点这些点能组成什么几何图形?探索并证明线段垂直平分线的判定你能再找一些到线段AB两端点的距离相等的点吗?能找到多少个到线段AB两端点距离相等的点?在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与A,B的距离相等的点都在直线l上,所以直线l可以看成与两点A、B的距离相等的所有点的集合.PABC解: AB=AC,∴点A在BC的垂直平分线. MB=MC, 点M在BC的垂直平分线上,∴直线AM是线段BC的垂直平分线.课堂练习练习3如图,AB=AC,MB=MC.直线AM是线段BC的垂直平分线吗?ABCDM(1)为什么任意取一点K,使点K与点C在直线两旁?尺规作图如何用尺规作图的方法经过直线外一点作已知直线的垂线?12DE(2)为什么要以大于的长为半径作弧?(3)为什么直线CF就是所求作的垂线?CABDKFE课堂练习练习4如图,过点P画∠AOB两边的垂线.ABOP11、 、 ,∴,∴ABAB==ACAC。。理由:理由:22、 、 ,∴,∴AA在线段在线段BCBC的中垂线上的中垂线上理由:理由:ADAD是是BCBC的中垂线的中垂线ABAB==ACAC线段垂直平分线上的点与这条线段垂直平分线上的点与这条线段两个端点的距离相等.线段两个端点的距离相等.与一条线段两个端点距离相等的点,与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。在这条线段的垂直平分线上。BBCCAADD3、如图,NMNM是线段是线段ABAB的中垂的中垂线线,,下列说法正确的有下列说法正确的有::。。①①AB⊥MN,②AD=DBAB⊥MN,②AD=DB,③,③MN⊥ABMN⊥AB,,④④MD=DNMD=DN,⑤,⑤ABAB是是MNMN的垂直平分的垂直平分线线ABMND①②③①②③44如图,若如图,若AC=12AC=12,,BC=7BC=7,,ABAB的垂直平分的垂直平分线交线交ABAB于于EE,交,交ACAC于于DD,求△,求△BCDBCD的周的周长。长。DCBEA解: EDED是线段是线段ABAB的垂直平分线的垂直平分线...