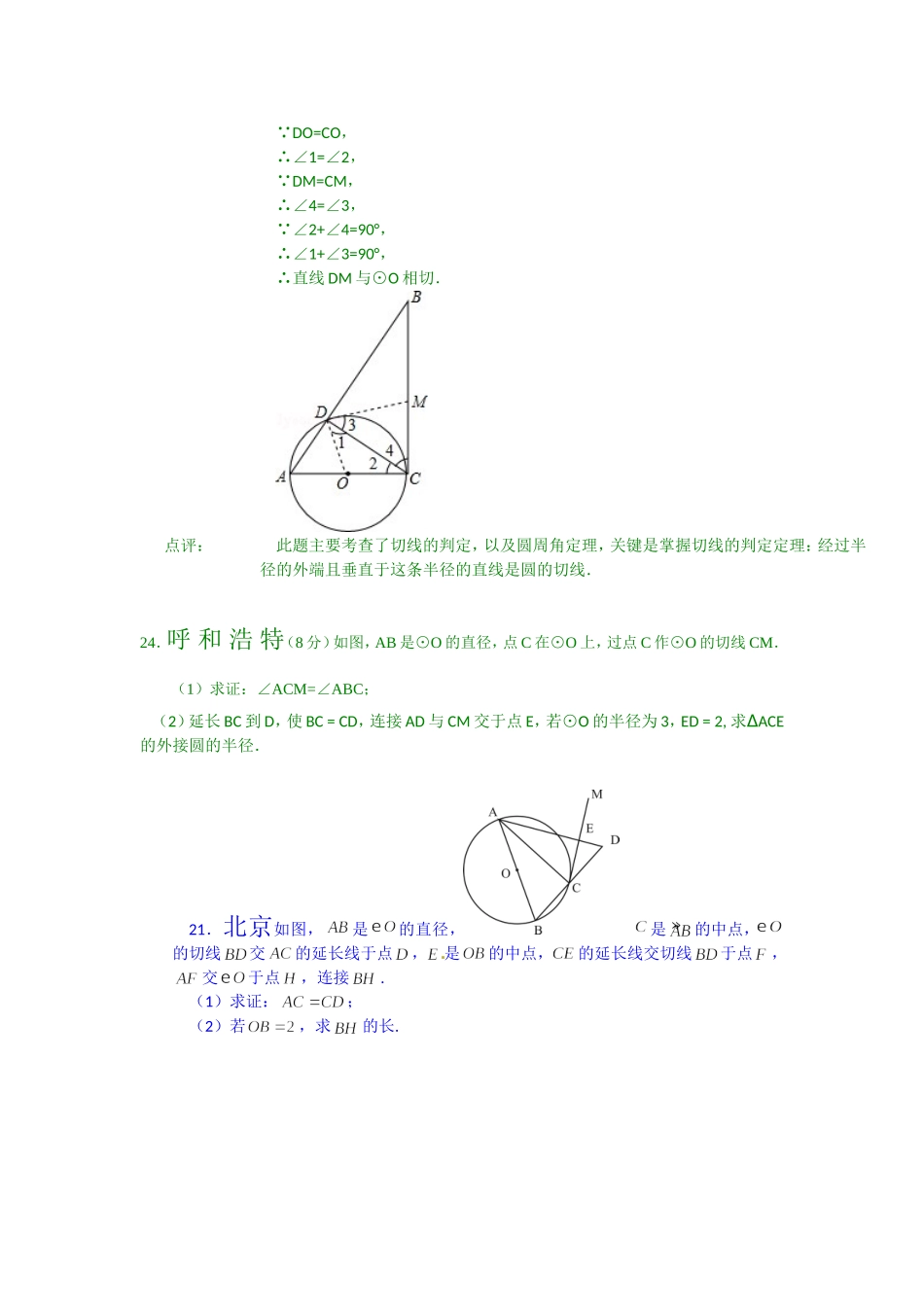
22.丽水(本题10分)如图,已知等边△ABC,AB=12,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD。(1)求证:DF是⊙O的切线;(2)求FG的长;(3)求tan∠FGD的值。26.(14分)(2014•毕节地区)如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.(1)求证:∠A=∠BCD;(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.考点:切线的判定分析:(1)根据圆周角定理可得∠ADC=90°,再根据直角三角形的性质可得∠A+∠DCA=90°,再由∠DCB+∠ACD=90°,可得∠DCB=∠A;(2)当MC=MD时,直线DM与⊙O相切,连接DO,根据等等边对等角可得∠1=∠2,∠4=∠3,再根据∠ACB=90°可得∠1+∠3=90°,进而证得直线DM与⊙O相切.解答:(1)证明: AC为直径,∴∠ADC=90°,∴∠A+∠DCA=90°, ∠ACB=90°,∴∠DCB+∠ACD=90°,∴∠DCB=∠A;(2)当MC=MD(或点M是BC的中点)时,直线DM与⊙O相切;解:连接DO, DO=CO,∴∠1=∠2, DM=CM,∴∠4=∠3, ∠2+∠4=90°,∴∠1+∠3=90°,∴直线DM与⊙O相切.点评:此题主要考查了切线的判定,以及圆周角定理,关键是掌握切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.24.呼和浩特(8分)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.(1)求证:∠ACM=∠ABC;(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求∆ACE的外接圆的半径.21.北京如图,是的直径,是的中点,的切线交的延长线于点,是的中点,的延长线交切线于点,交于点,连接.(1)求证:;(2)若,求的长.OHEFCBAD7.(3分)(2014•临夏)已知⊙O的半径是6cm,点O到同一平面内直线l的距离为5cm,则直线l与⊙O的位置关系是(A)A.相交B.相切C.相离D.无法判断考点:直线与圆的位置关系.分析:设圆的半径为r,点O到直线l的距离为d,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离,从而得出答案.解答:解:设圆的半径为r,点O到直线l的距离为d,d=5 ,r=6,d∴<r,∴直线l与圆相交.故选A.点评:本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定.27.(10分)(2014•临夏)如图,RtABC△中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.(1)求证:DE是半圆⊙O的切线.(2)若∠BAC=30°,DE=2,求AD的长.考点:切线的判定.专题:计算题.分析:(1)连接OD,OE,由AB为圆的直径得到三角形BCD为直角三角形,再由E为斜边BC的中点,得到DE=BE=DC,再由OB=OD,OE为公共边,利用SSS得到三角形OBE与三角形ODE全等,由全等三角形的对应角相等得到DE与OD垂直,即可得证;(2)在直角三角形ABC中,由∠BAC=30°,得到BC为AC的一半,根据BC=2DE求出BC的长,确定出AC的长,再由∠C=60°,DE=EC得到三角形EDC为等边三角形,可得出DC的长,由ACCD﹣即可求出AD的长.解答:(1)证明:连接OD,OE,AB 为圆O的直径,ADB=BDC=90°∴∠∠,在RtBDC△中,E为斜边BC的中点,DE=BE∴,在△OBE和△ODE中,,OBEODE∴△△≌(SSS),ODE=ABC=90°∴∠∠,则DE为圆O的切线;(2)在RtABC△中,∠BAC=30°,BC=∴AC,BC=2DE=4 ,AC=8∴,又 ∠C=60°,DE=DC,DEC∴△为等边三角形,即DC=DE=2,则AD=ACDC=6﹣.点评:此题考查了切线的判定,以及全等三角形的判定与性质,熟练掌握切线的判定方法是解本题的关键.18、梅州市本题满分8分。如图5,在⊿ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C。(1)求证:AB与⊙O相切;(2)若∠AOB=120°,AB=4,求⊙O的面积。(1)证明:连接OC,(2) C是边AB的中点,AB=4∴BC=2 OA=OB,C是边AB的中点∴中线OC可以表示高和∠AOB的平分线∴在Rt⊿BOC中,∠BOC=60°,即有OC==2S⊙O=4π24、如题24图,⊙是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.⑴若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)⑵...