立体几何+第九讲：直线、平面平行的性质课件--名师微课堂（自制）VIP免费

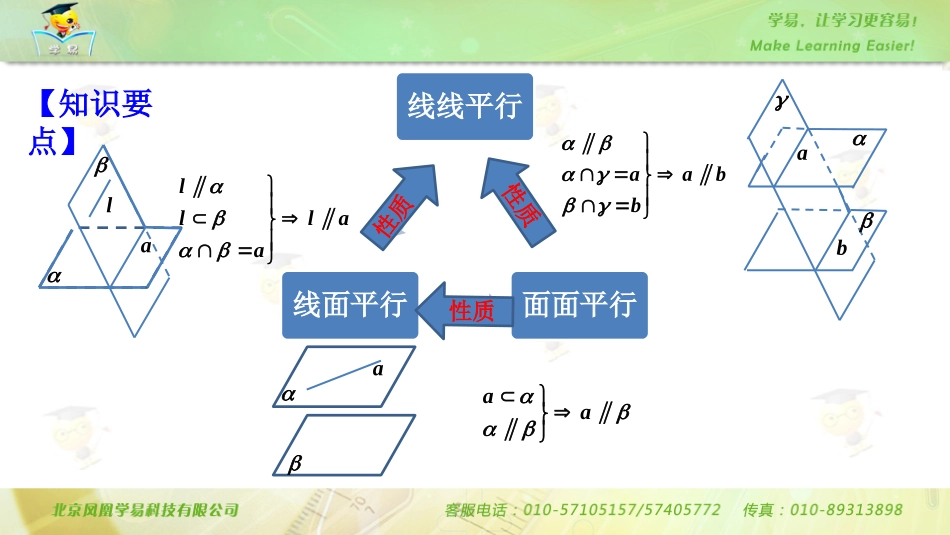
直线、平面平行的性质讲师：徐敬才知识要点【知识要点】线线平行面面平行线面平行性质lllaaal性质aaa性质aabbab典题剖析【解析】∵HN∥BD，HF∥DD1，∴平面NHF∥平面B1BDD1．故线段FH上任一点M与N相连，都有MN∥平面B1BDD1，故填M∈线段FH.【方法归纳】过空间一点找与已知平面平行的直线时，一般过该点作出与已知平面平行的平面，然后找此平面与限定的直线的交点或限定平面的交线．【证明】如图，∵平面ADD1A1∥平面BCC1B1，且平面ADD1A1∩平面α=A1D，平面BCC1B1∩平面α=CQ，∴A1D∥CQ.又因为A1A∥BQ，AD∥BC，∴△A1AD∽△QBC．∴1112BQBQBCBBAAAD，∴Q为BB1的中点．1A1B1C1DABCDQ【解析】存在点E，且E为AB的中点．证明如下：如图，取BB1的中点F，连接DF，则DF∥B1C1．∵AB的中点为E，连接EF，则EF∥AB1．B1C1与AB1是相交直线，∴平面DEF∥平面AB1C1．而DE⊂平面DEF，∴DE∥平面AB1C1．FE【方法归纳】解决探究性问题一般要采用执果索因的方法，假设求解的结果存在，从这个结果出发，寻找使这个结论成立的充分条件，如果找到了符合题目结果要求的条件，则存在；如果找不到符合题目结果要求的条件（出现矛盾），则不存在．【解析】在PD上存在一点E，且E为PD的中点，使得NM∥平面ACE．证明如下：如图，取PD的中点E，连接NE，EC因为N，E分别为PA，PD的中点，所以NE平行且等于12AD．又在平行四边形ABCD中，CM平行且等于12AD．所以NE平行且等于MC，即四边形MCEN是平行四边形．所以NM∥EC．又EC⊂平面ACE，NM⊄平面ACE，所以MN∥平面ACE，即在PD上存在一点E，且E为PD的中点，使得NM∥平面ACE．E技巧传播结合空间平行关系，利用平行的性质，设计开放型试题是近几年高考命题的一个方向.解决探究性问题一般要采用执果索因的方法，假设求解的结果存在，从这个结果出发，寻找使这个结论成立的充分条件，如果找到了符合题目结果要求的条件，则存在；如果找不到符合题目结果要求的条件（出现矛盾），则不存在．找的过程，实际就是做平面找交点或交线的过程，要总结规律，提炼模板.陷阱规避【正解】图①中，∵平面MNP∥平面β，∴AB∥平面MNP；图②中，连接底面对角线交MP与点E，连接NE，假设AB∥平面MNP，由线面平行的性质，一定有AB∥NE，而N为所在棱的中点，E为面对角线的四等分点，显然AB不与NE平行，所以假设错误；图③中，连接面对角线EF，如图，易知MP∥EF，且AB∥EF，所以AB∥MP，又AB不在平面MNP内，所以AB∥平面MNP；图④中，过M点作ME∥AB，假设AB∥平面MNP，由线面平行的性质，ME应该在平面MNP内，而显然点E不在平面内，所以假设错误．正确序号为①③.EEFE【误解】若不注意平面的延展性，或应用定理时忽略某些条件会导致错解.