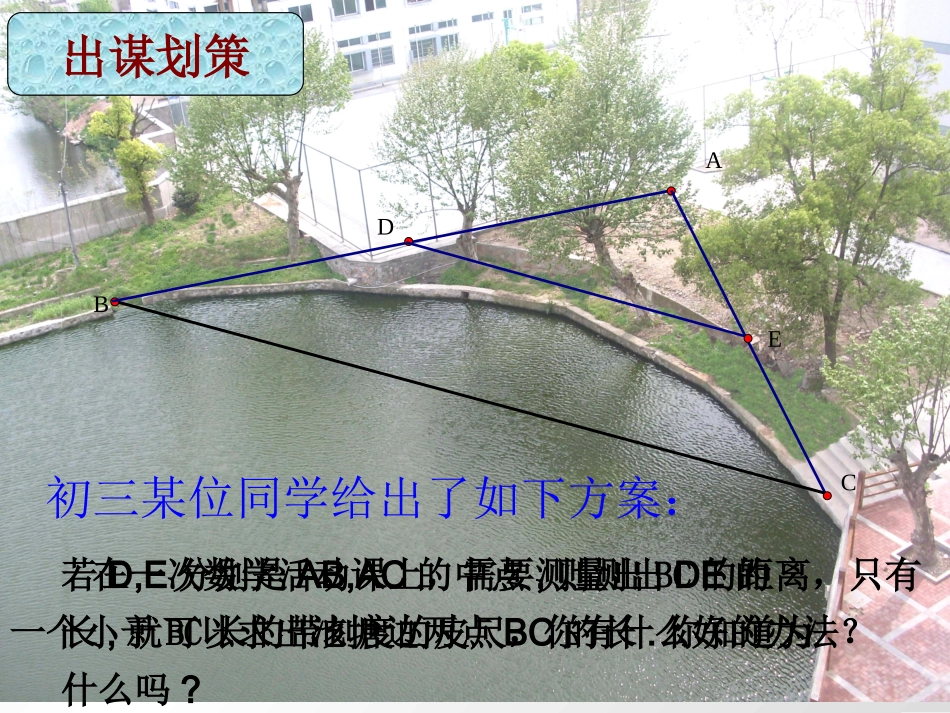
6.3三角形的中位线俞斌勋ABCDE美丽校园在一次数学活动课上,需要测量出BC的距离,只有一个小于BC长的带刻度的皮尺,你有什么好的办法?初三某位同学给出了如下方案:若D,E分别是AB,AC的中点,则测出DE的长,就可以求出池塘边两点BC的长.你知道为什么吗?出谋划策(1)掌握三角形的中位线的概念;(2)探索三角形的中位线的性质;(3)会利用三角形中位线性质解决简单的实际问题.学习目标温馨提示连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线 D、E分别为AB、AC的中点∴DE为△ABC的中位线三角形的中位线和三角形的中线不同EDFACB获取新知你还能画出几条三角形的中位线?•三角形中位线的两个端点都是三角形边的中点。•三角形中线只有一个端点是边的中点,另一个端点是三角形的一个顶点。ABCDEF···中位线与中线的区别3、你能用推理的方法证明四边形DBCF是平行四边形吗,试试看?BFDACE探究活动一1、将一个三角形沿其中一条中位线剪开得到一个小三角形和一个梯形,你能否利用这两个图形拼出另外一个我们熟悉的图形呢?2、在拼成平行四边形时,我们能否看成是小三角形的某个变换得到的呢?BFDACE猜一猜:△ABC的中位线DE与BC的关系怎样?(从位置和数量关系猜想)获取新知DEBC,∥BCDE21即:三角形的中位线平行于第三边,并且等于第三边的一半。你能验证你的猜想吗?BFDACE已知:如图,D、E分别是△ABC的边AB、AC的中点.求证:DEBC∥,BCDE21三角形的中位线平行于第三边三角形的中位线平行于第三边,,并且等于第三边的一半并且等于第三边的一半..证明:如图,以E为旋转中心,把△ADE绕点E按顺时针方向旋转1800,得到△CEF,则D、E、F同在一直线上,DE=EF,且△ADE≌△CFE又 AD=BD=CF∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形)∴DE∥BC且DE=1/2BC∴∠ADE=F,AD=CF∠∴ADCF∥三角形的中位线平行于第三边,并且等于第三边的一半.三角形的中位线平行于第三边,并且等于第三边的一半.几何语言: DE是△ABC的中位线∴DE∥BC,且DE=1/2BC(三角形的中位线平行于第三边,并且等于它的一半)CEDBA①证明平行问题②证明一条线段是另一条线段的两倍或一半用途ABCDE初三某位同学给出了如下方案:若D,E分别是AB,AC的中点,则测出DE的长,就可以求出池塘边两点BC的长.你知道为什么吗?问题解决ACBEDF初试身手练习1.如图,在△ABC中,D、E分别是AB、AC的中点①若∠ADE=65°,则∠B=度,为什么?②若BC=8cm,则DE=cm,为什么?654③若AC=4cm,BC=6cm,AB=8cm,则△DEF的周长=______练习1.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点9cm④若△ABC的周长为24,△DEF的周长是_____121、三角形三条中位线围成的三角形的周长与原三角形的周长的关系?探究活动二2、三角形三条中位线围成的三角形的面积与原三角形的面积的关系?⑤图中有_____个平行四边形⑥若△ABC的面积为24,△DEF的面积是_____3366通过刚才的学习,我们探索并发现连接任意三角形三边中点所得的三角形的部分规律,对于任意四边形,连接四边中点所得到的四边形又有何规律呢?请你动手画一画!ABCDEFGHCEDBA探究活动三已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.ABCDEFGH证明:如图,连接AC EF是△ABC的中位线AC21//EF同理得:AC21//GHEF//GH∴四边形EFGH是平行四边形探究活动三在四边形ABCD中,AB=CD,M,N,P分别AD,BC,BD的中点。求证:∠PNM=PMN.∠挑战自我三角形的中位线平行于第三边三角形的中位线平行于第三边,,并且等于第并且等于第三边的一半三边的一半2、三角形中位线定理1、三角形中位线的定义3、会利用三角形中位线定理解决一些简单的实际问题谈谈收获1.已知:如图,DE,EF是△ABC的两条中位线.求证:四边形BFED是平行四边形.2.如图,DE是△ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.DBCFEA(第1题)FEDCBAO(第2题)补充练习三角形的中位线平行于第三边,并且等于第三边的一半ABCDEF已知:在△ABC中,DE是△ABC的中位线求证:DE∥BC,且DE=1/2BC。证法2:如图,延长DE到F,使EF=DE,连结CF. DE=EF、∠AED=CEF∠、A...