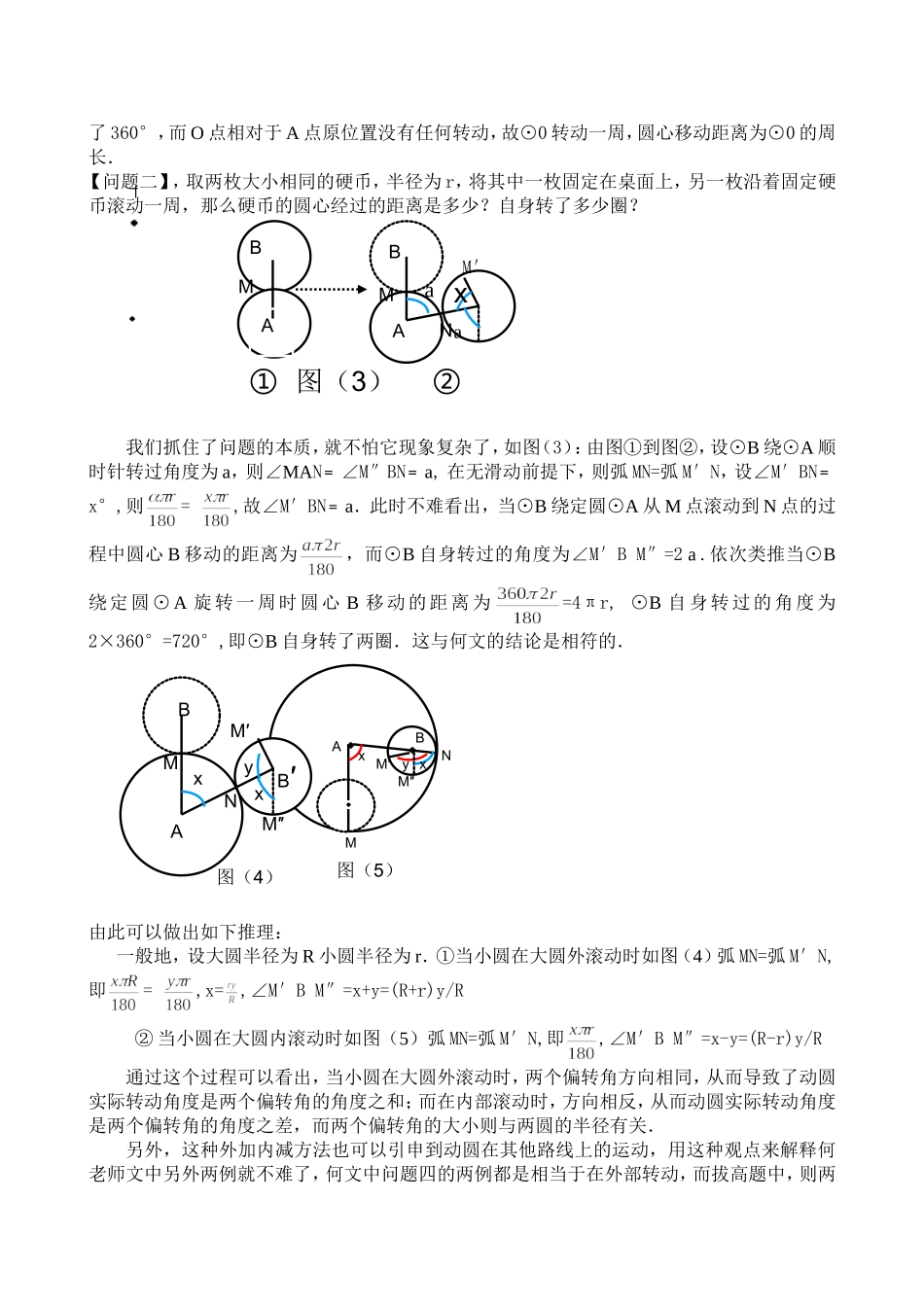
日期:2009.8.7.所投栏目:辅导参考.联系方式:15972561623.E-mail:932631151@qq163.com也谈硬币能滚多远湖北省郧县高庙中学(442519)王显翠《中小学数学》2009版1-2期p54页何秀岩老师的《硬币能滚多远》一文中,再次把双动圆之类问题呈现到了大家面前.就象何老师文中所言,这种问题很有趣,与圆的知识联系紧密,有助与激发学生的学习兴趣.但学生难以理解,更不易于操作.其实这类问题,不仅北师大版教材中才出现,早在1994年10月人教版初中《几何》第三册189页就出现了这个问题,历时七年,在2001年的版本中被删除.问题的原因关键在于一线的教师们争议颇多,没有人能真正领会数学家源创数学知识时的动机,去抓住问题的本质和规律,从眼花潦乱的客观现象中抽象出基本实质,从而给学生一个明确而通俗的解释.这些年来,我也和同事们一起探讨过这个问题,也读过类似何老师这样的文章.这里的基本事实、基本结论是大家都认可的,但是面对著此模糊的,笼统的解释,总觉得不具备足够的说服力和可操作性.不象何老师文中所说那样学生动手试一试,一做便有了答案.一些总结性的结论,也同样让人费解.以下是我对此事一点浅薄的理解,以供大家参考.首先,这个问题不是一个单一的数学问题,应该结合其他学科学辩证的去理解,下面我们先看这样一个现象:如图(1),站在A点看B点,B点在A点的正东方,当B点绕A点逆时针旋转30°时,B点在A点的东偏北30°方向上,距离不变;当B点不动,A点绕B点逆时针旋转30°达到A′时,站在A′点位置看B点,仍然是B点在A点的东偏北30°方向上,距离不变;若A、B两点都先后绕对方原位置逆时针旋转30°,则站在A′处看B′,显然已是东偏北60°了;反之若B点绕A点原位置逆时针旋转30°,而A点绕B点原位置顺时针旋转30°,则B′点仍在点的正东方.这其实就告诉我们前边问题中,现象与本质之间的差异了.【问题一】:一枚半径为R的硬币沿直线滚动一周,圆心移动的距离是多远?在这个问题中,看似简单,但其过程分解后并不简单.如图(2)所示,在⊙0运动的四个阶段圆上某点(切点)始终在0点正下方,即偏转角为0,而半径0A依次转过90°、180°、270°、360°,最后A点又回到切点位置.也就是说,A点相对于O点原位置转AB′B30°60°图(1)30°A′A′30°了360°,而O点相对于A点原位置没有任何转动,故⊙0转动一周,圆心移动距离为⊙0的周长.【问题二】,取两枚大小相同的硬币,半径为r,将其中一枚固定在桌面上,另一枚沿着固定硬币滚动一周,那么硬币的圆心经过的距离是多少?自身转了多少圈?我们抓住了问题的本质,就不怕它现象复杂了,如图(3):由图①到图②,设⊙B绕⊙A顺时针转过角度为a,则∠MAN﹦∠M″BN﹦a,在无滑动前提下,则弧MN=弧M′N,设∠M′BN﹦x°,则=,故∠M′BN﹦a.此时不难看出,当⊙B绕定圆⊙A从M点滚动到N点的过程中圆心B移动的距离为,而⊙B自身转过的角度为∠M′BM″=2a.依次类推当⊙B绕定圆⊙A旋转一周时圆心B移动的距离为=4πr,⊙B自身转过的角度为2×360°=720°,即⊙B自身转了两圈.这与何文的结论是相符的.由此可以做出如下推理:一般地,设大圆半径为R小圆半径为r.①当小圆在大圆外滚动时如图(4)弧MN=弧M′N,即=,x=,∠M′BM″=x+y=(R+r)y/R②当小圆在大圆内滚动时如图(5)弧MN=弧M′N,即,∠M′BM″=x-y=(R-r)y/R通过这个过程可以看出,当小圆在大圆外滚动时,两个偏转角方向相同,从而导致了动圆实际转动角度是两个偏转角的角度之和;而在内部滚动时,方向相反,从而动圆实际转动角度是两个偏转角的角度之差,而两个偏转角的大小则与两圆的半径有关.另外,这种外加内减方法也可以引申到动圆在其他路线上的运动,用这种观点来解释何老师文中另外两例就不难了,何文中问题四的两例都是相当于在外部转动,而拔高题中,则两ABMNM′M″xyx图(5)ABABaMNMax①②图(3)M′ABB′NMxxM″图(4)yM′种转动成分兼而有之.总之,在教学中,教给学生用一种浅显的思维方式去思考一些深刻的道理,不仅可以使复杂的问题简单化,而且可以引发学生的探究兴趣和创新精神.反之机械的灌输,至酷的训练,反而窒息了学生的活力,束缚人类创造才能的正常发挥.