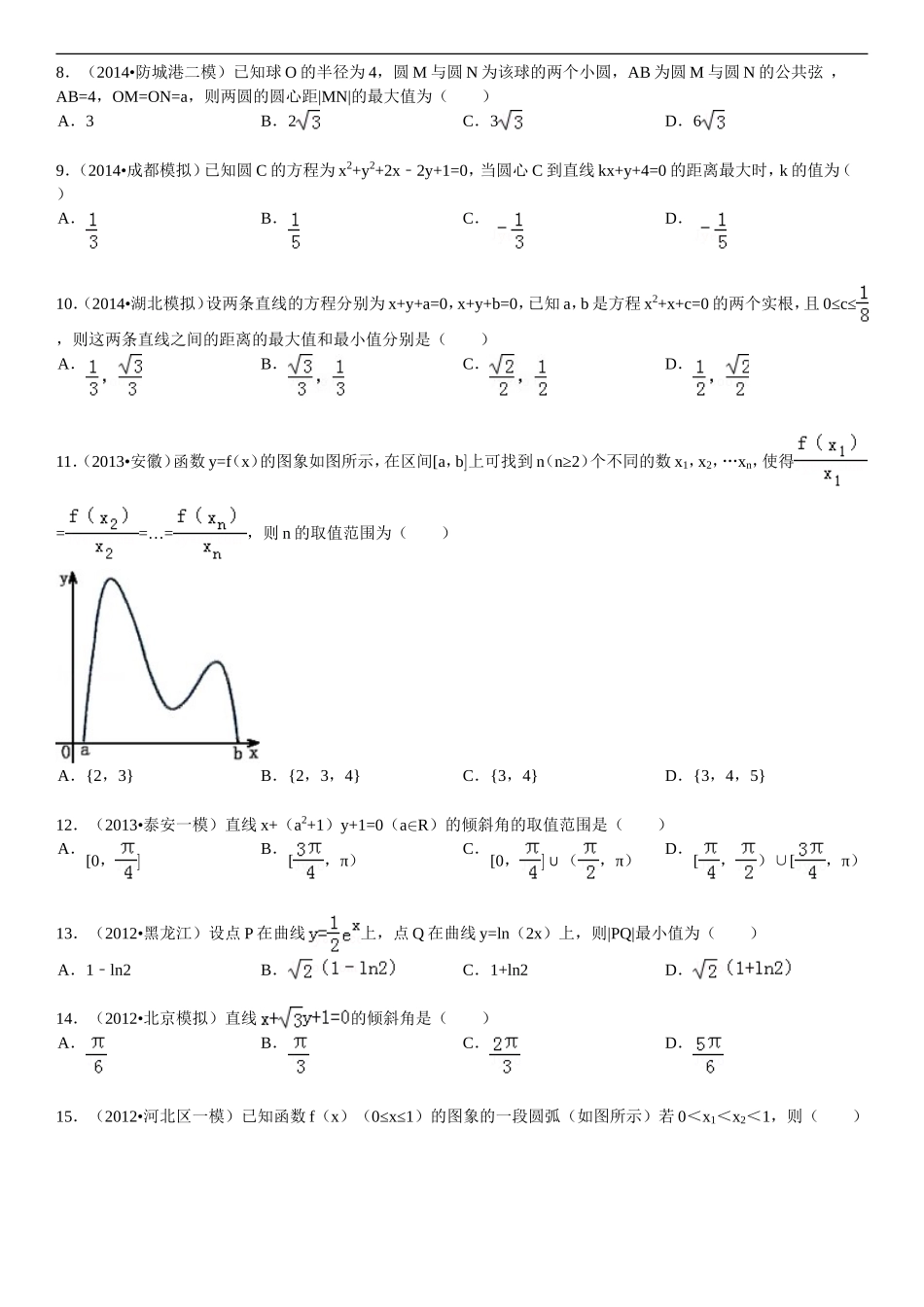
一.选择题(共28小题)1.(2014•四川)设m∈R,过定点A的动直线x+my=0和过定点B的直线mxym+3=0﹣﹣交于点P(x,y),则|PA|+|PB|的取值范围是()A.[,2]B.[,2]C.[,4]D.[2,4]2.(2014•丰台区二模)过抛物线y2=2px(p>0)的焦点F且倾斜角为60°的直线l与抛物线在第一、四象限分别交于A、B两点,则的值等于()A.5B.4C.3D.23.(2014•银川模拟)斜率为2的直线l过双曲线﹣=1(a>0,b>0)的右焦点,且与双曲线的左右两支分别相交,则双曲线的离心率e的取值范围是()A.e<B.1<e<C.1<e<D.e>4.(2014•包头一模)已知函数f(x)=ln(x+1),x∈(0,+∞),下列结论错误的是()A.∀x1,x2∈(0,+∞),(x2x﹣1)[f(x2)﹣f(x1)]≥0B.∀x1∈(0,+∞),∃x2∈(0,+∞),x2f(x1)>x1f(x2)C.∀x1∈(0,+∞),∃x2∈(0,+∞),f(x2)﹣f(x1)<x2x﹣1D.∃x1,x2∈(0,+∞),5.(2014•蚌埠二模)已知两条直线y=ax2﹣和3x﹣(a+2)y+1=0互相平行,则a等于()A.1或﹣3B.1﹣或3C.1或3D.1﹣或﹣36.(2014•东昌区二模)已知b>0,直线(b2+1)x+ay+2=O与直线xb﹣2y1=O﹣互相垂直,则ab的最小值等于()A.1B.2C.D.7.(2014•甘肃二模)已知点P在直线x+2y1=0﹣上,点Q在直线x+2y+3=0上,PQ的中点为M(x0,y0),且y0>x0+2,则的取值范围是()A.B.C.D.8.(2014•防城港二模)已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,OM=ON=a,则两圆的圆心距|MN|的最大值为()A.3B.2C.3D.69.(2014•成都模拟)已知圆C的方程为x2+y2+2x2y+1=0﹣,当圆心C到直线kx+y+4=0的距离最大时,k的值为()A.B.C.D.10.(2014•湖北模拟)设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a,b是方程x2+x+c=0的两个实根,且0≤c≤,则这两条直线之间的距离的最大值和最小值分别是()A.B.C.D.11.(2013•安徽)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…xn,使得==…=,则n的取值范围为()A.{2,3}B.{2,3,4}C.{3,4}D.{3,4,5}12.(2013•泰安一模)直线x+(a2+1)y+1=0(a∈R)的倾斜角的取值范围是()A.[0,]B.[,π)C.[0,]∪(,π)D.[,)∪[,π)13.(2012•黑龙江)设点P在曲线上,点Q在曲线y=ln(2x)上,则|PQ|最小值为()A.1ln2﹣B.C.1+ln2D.14.(2012•北京模拟)直线的倾斜角是()A.B.C.D.15.(2012•河北区一模)已知函数f(x)(0≤x≤1)的图象的一段圆弧(如图所示)若0<x1<x2<1,则()A.B.C.D.前三个判断都不正确16.(2015•开封模拟)将边长为2的等边△PAB沿x轴正方向滚动,某时刻P与坐标原点重合(如图),设顶点P(x,y)的轨迹方程是y=f(x),关于函数y=f(x)的有下列说法:f①(x)的值域为[0,2];f②(x)是周期函数;f③(4.1)<f(π)<f(2013);∫④f(x)dx=.其中正确的说法个数为()A.0B.1C.2D.317.(2014•东营一模)若圆C经过(1,0),(3,0)两点,且与y轴相切,则圆C的方程为()A.(x2﹣)2+(y±2)2=3B.C.(x2﹣)2+(y±2)2=4D.18.(2014•浦东新区三模)若当P(m,n)为圆x2+(y1﹣)2=1上任意一点时,等式m+n+c=0恒成立,则c的取值范围是()A.1﹣﹣≤c≤1﹣B.1≤c≤﹣+1C.c≤﹣1﹣D.c≥1﹣19.(2014•南昌二模)方程(x2+y22x﹣)=0表示的曲线是()A.一个圆和一条直线B.一个圆和一条射线C.一个圆D.一条直线20.(2014•黄冈模拟)在等腰梯形ABCD中,E,F分别是底边AB,CD的中点,把四边形AEFD沿直线EF折起后所在的平面记为α,P∈α,设PB,PC与α所成的角分别为θ1,θ2(θ1,θ2均不等于零).若θ1=θ2,则点P的轨迹为()A.直线B.圆C.椭圆D.抛物线21.(2014•南开区二模)设圆C:x2+y2=3,直线l:x+3y6=0﹣,点P(x0,y0)∈l,存在点Q∈C,使∠OPQ=60°(O为坐标原点),则x0的取值范围是()A.B.[0,1]C.D.22.(2014•福建模拟)设双曲线的离心率为,右焦点为F(c,0),方程ax2bx﹣﹣c=0的两个实根分别为x1和x2,则点P(x...