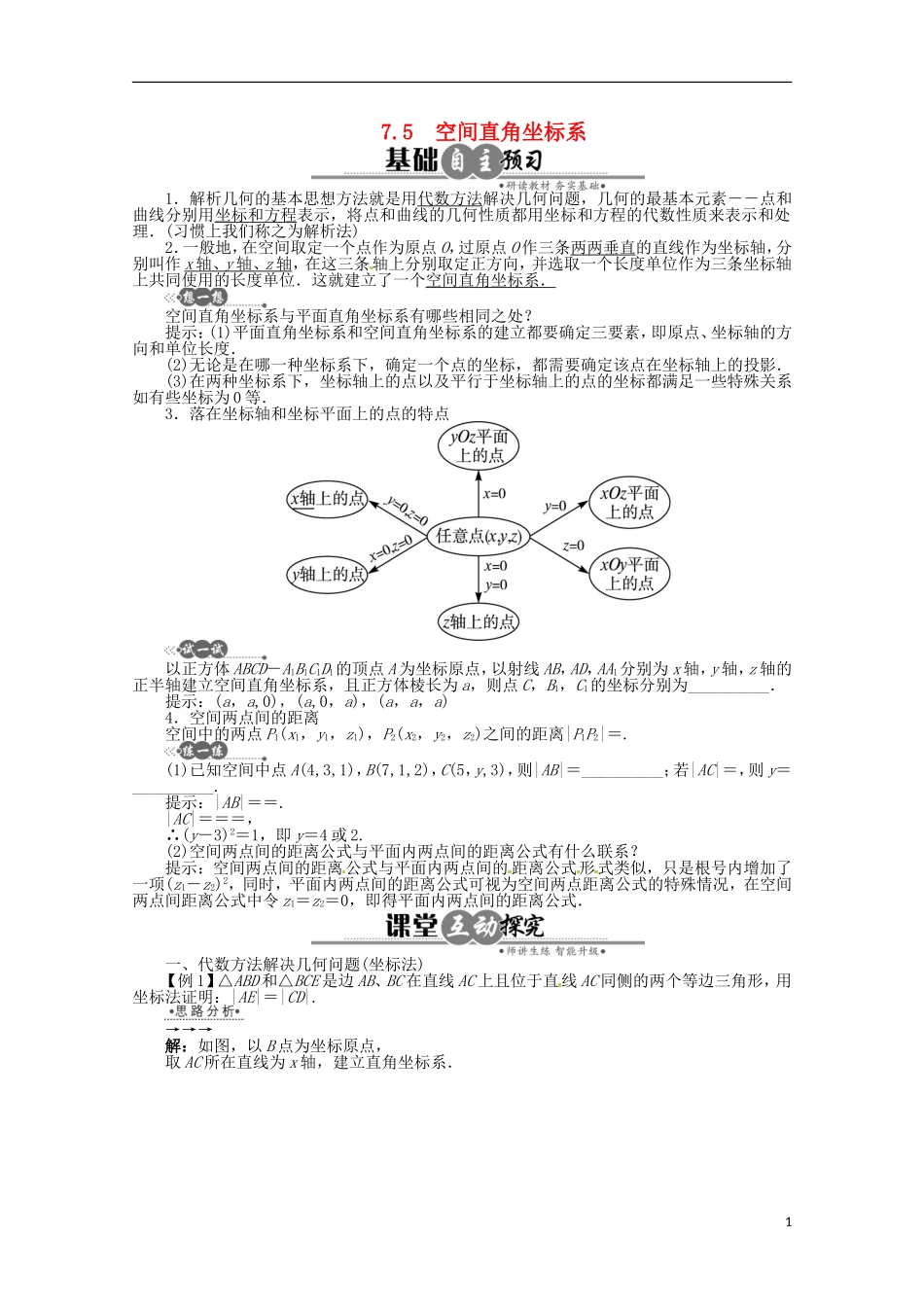
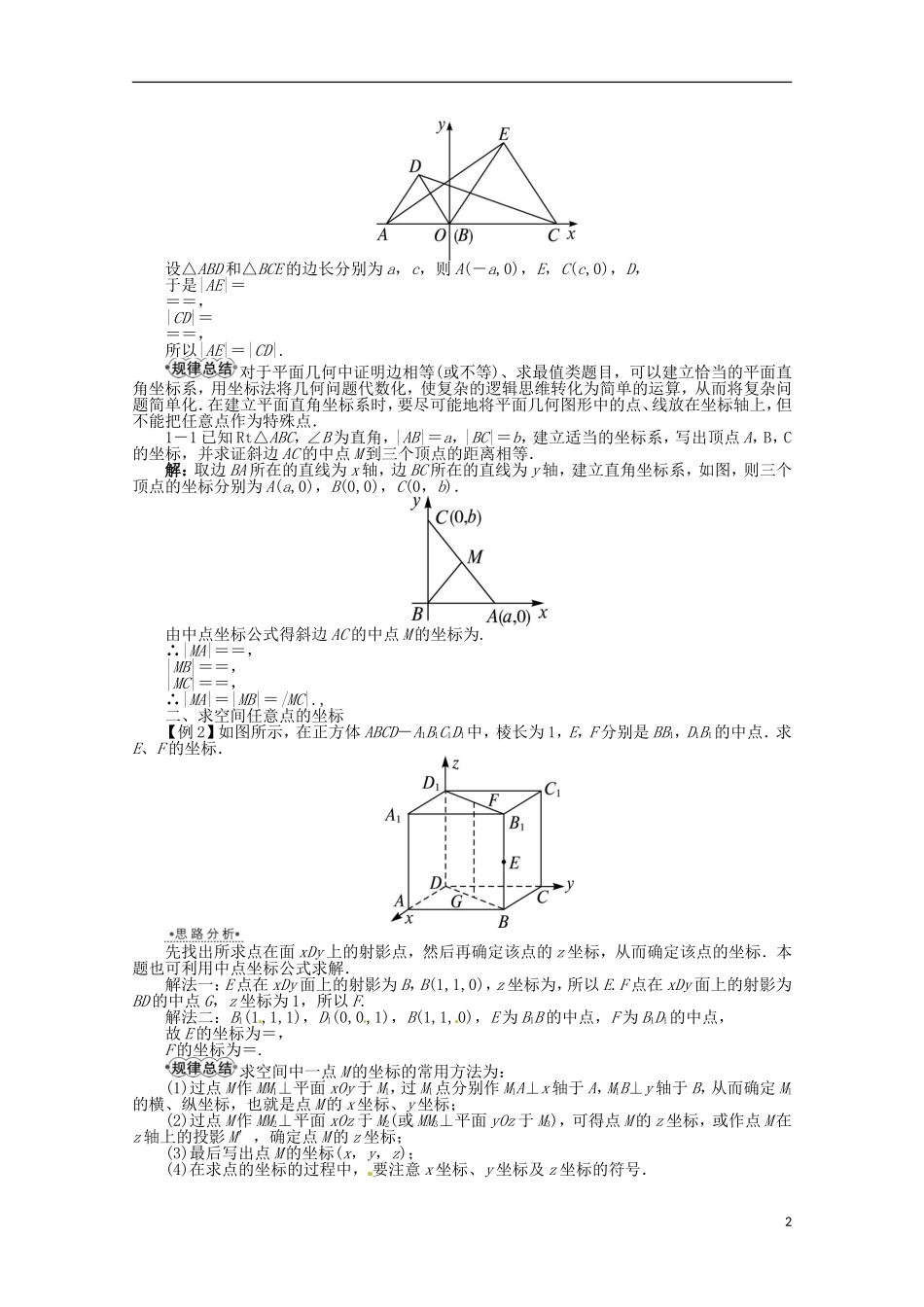
7.5空间直角坐标系1.解析几何的基本思想方法就是用代数方法解决几何问题,几何的最基本元素--点和曲线分别用坐标和方程表示,将点和曲线的几何性质都用坐标和方程的代数性质来表示和处理.(习惯上我们称之为解析法)2.一般地,在空间取定一个点作为原点O,过原点O作三条两两垂直的直线作为坐标轴,分别叫作x轴、y轴、z轴,在这三条轴上分别取定正方向,并选取一个长度单位作为三条坐标轴上共同使用的长度单位.这就建立了一个空间直角坐标系.空间直角坐标系与平面直角坐标系有哪些相同之处?提示:(1)平面直角坐标系和空间直角坐标系的建立都要确定三要素,即原点、坐标轴的方向和单位长度.(2)无论是在哪一种坐标系下,确定一个点的坐标,都需要确定该点在坐标轴上的投影.(3)在两种坐标系下,坐标轴上的点以及平行于坐标轴上的点的坐标都满足一些特殊关系如有些坐标为0等.3.落在坐标轴和坐标平面上的点的特点以正方体ABCD-A1B1C1D1的顶点A为坐标原点,以射线AB,AD,AA1分别为x轴,y轴,z轴的正半轴建立空间直角坐标系,且正方体棱长为a,则点C,B1,C1的坐标分别为__________.提示:(a,a,0),(a,0,a),(a,a,a)4.空间两点间的距离空间中的两点P1(x1,y1,z1),P2(x2,y2,z2)之间的距离|P1P2|=.(1)已知空间中点A(4,3,1),B(7,1,2),C(5,y,3),则|AB|=__________;若|AC|=,则y=__________.提示:|AB|==.|AC|===,∴(y-3)2=1,即y=4或2.(2)空间两点间的距离公式与平面内两点间的距离公式有什么联系?提示:空间两点间的距离公式与平面内两点间的距离公式形式类似,只是根号内增加了一项(z1-z2)2,同时,平面内两点间的距离公式可视为空间两点距离公式的特殊情况,在空间两点间距离公式中令z1=z2=0,即得平面内两点间的距离公式.一、代数方法解决几何问题(坐标法)【例1】△ABD和△BCE是边AB、BC在直线AC上且位于直线AC同侧的两个等边三角形,用坐标法证明:|AE|=|CD|.→→→解:如图,以B点为坐标原点,取AC所在直线为x轴,建立直角坐标系.1设△ABD和△BCE的边长分别为a,c,则A(-a,0),E,C(c,0),D,于是|AE|===,|CD|===,所以|AE|=|CD|.对于平面几何中证明边相等(或不等)、求最值类题目,可以建立恰当的平面直角坐标系,用坐标法将几何问题代数化,使复杂的逻辑思维转化为简单的运算,从而将复杂问题简单化.在建立平面直角坐标系时,要尽可能地将平面几何图形中的点、线放在坐标轴上,但不能把任意点作为特殊点.1-1已知Rt△ABC,∠B为直角,|AB|=a,|BC|=b,建立适当的坐标系,写出顶点A,B,C的坐标,并求证斜边AC的中点M到三个顶点的距离相等.解:取边BA所在的直线为x轴,边BC所在的直线为y轴,建立直角坐标系,如图,则三个顶点的坐标分别为A(a,0),B(0,0),C(0,b).由中点坐标公式得斜边AC的中点M的坐标为.∴|MA|==,|MB|==,|MC|==,∴|MA|=|MB|=|MC|.,二、求空间任意点的坐标【例2】如图所示,在正方体ABCD-A1B1C1D1中,棱长为1,E,F分别是BB1,D1B1的中点.求E、F的坐标.先找出所求点在面xDy上的射影点,然后再确定该点的z坐标,从而确定该点的坐标.本题也可利用中点坐标公式求解.解法一:E点在xDy面上的射影为B,B(1,1,0),z坐标为,所以E.F点在xDy面上的射影为BD的中点G,z坐标为1,所以F.解法二:B1(1,1,1),D1(0,0,1),B(1,1,0),E为B1B的中点,F为B1D1的中点,故E的坐标为=,F的坐标为=.求空间中一点M的坐标的常用方法为:(1)过点M作MM1⊥平面xOy于M1,过M1点分别作M1A⊥x轴于A,M1B⊥y轴于B,从而确定M1的横、纵坐标,也就是点M的x坐标、y坐标;(2)过点M作MM2⊥平面xOz于M2(或MM3⊥平面yOz于M3),可得点M的z坐标,或作点M在z轴上的投影M′,确定点M的z坐标;(3)最后写出点M的坐标(x,y,z);(4)在求点的坐标的过程中,要注意x坐标、y坐标及z坐标的符号.22-1在空间直角坐标系中,已知点P(1,,),过P作平面yOz的垂线PQ,则垂足Q的坐标为().A.(0,,0)B.(0,,)C.(1,0,)D.(1,,0)解析:根据空间直角坐标系的概念知,yOz平面上点Q的x坐标为0,y坐标、z坐标与点P的y坐标、z坐标分别相等,∴Q...