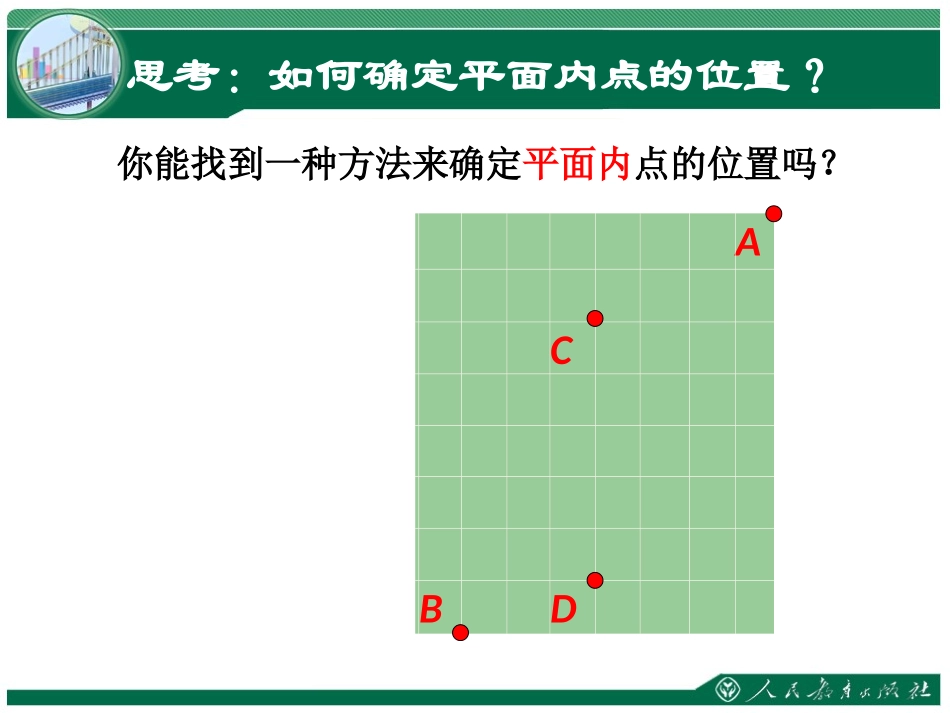
第七章平面直角坐标系7.1.2平面直角坐标系(第1课时)思考:如何确定直线上点的位置?规定了原点、正方向、单位长度的直线叫做数轴。数轴上的点与实数是一一对应的。数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标。例如,点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。·01234-3-2-1原点••ABACBD你能找到一种方法来确定平面内点的位置吗?思考:如何确定平面内点的位置?ACDB-3-2-1123-44xx轴(横轴)y轴(纵轴)-1-2-3-41234yO原点我们可以在平面内画两条互相垂直、原点重合的数轴组成平面直角坐标系。1、两条数轴2、互相垂直3、原点重合建立平面直角坐标系平面直角坐标系的定义在平面内,两条互相垂直、原点重合的数轴组成平面直角坐标系。-3-2-1123o-1-2-3123xy正方向:数轴向右与向上的方向y轴或纵轴:竖直的数轴坐标轴:x轴或横轴:水平的数轴原点:两条数轴的公共原点O·A31425-2-4-1-3012345-4-3-2-1x横轴y纵轴A的横坐标为4A的纵坐标为2有序数对(4,2)就叫做A的坐标·B(-4,1)记作:(4,2)横坐标在前纵坐标在后点的坐标发现规律:坐标平面内的点和有序实数对是一一对应的。ACDB-3-2-1123-44x-1-2-3-41234yO应用解:A(3,4)B(-3,-4)C(0,2)D(0,-3)1、写出图中各点的坐标:练习ABCD解:A(2,3)B(-3,2)C(-4,-2)D(3,-4)M(1,0)N(-3,0)P(0,3)Q(0,-4)R(0,0)思考:坐标轴上点的坐标有什么规律?3、原点的坐标为(0,0)原点既在x轴上,又在y轴上,是x轴和y轴的交点。2、y轴上点可记作(_,y)即y轴上点的横坐标为0。1、x轴上点可记作(x,_)即x轴上点的纵坐标为0。00(0,3)(0,0)(0,-4)(1,0)(-3,0)-55-3-44-23-121-66oX5-2-3-4-132416yy轴或纵轴x轴或横轴原点第一象限第二象限第三象限第四象限象限的划分象限:两条坐标轴把平面分成四个部分。注意:坐标轴上的点不属于任何象限。x2、写出图中各点的坐标,并指出位于哪个象限:(3,2)(-2,1)(-4,-3)(1,-2)(2,3)012345-4-3-2-1·B31425-2-4-1-3y·C·A·E·D·练习四个象限内点的坐标的符号有什么规律?(+,+)(-,+)(-,-)(+,-)思考根据点所在的位置,用“+”“-”或“0”填表:点的位置横坐标符号纵坐标符号在第一象限在第二象限在第三象限在第四象限在x轴上在正半轴上在负半轴上在y轴上在正半轴上在负半轴上原点++++00++0000------发现规律xO123-1-2-312-1-2-3y在平面直角坐标系中找出坐标为(3,-2)的点AA由坐标找点由坐标找点的方法:1.找到表示横坐标与纵坐标的点,2.过这两点分别作x轴与y轴的垂线,3.垂线的交点就是该坐标对应的点。31425-2-4-1-3012345-4-3-2-1xy·B·D·C例1在直角坐标系中描出下列各点:A(4,5)B(-2,3)C(-4,-1)D(2.5,-2)E(0,-4)·AE·例题讲解解:如图所示1.写出下图中点A,B,C,D,E,F的坐标.练习解:A(-2,-2)B(-5,4)C(5,-4)D(0,-3)E(2,5)F(-3,0)2.在图中描出下列各点:练习L(-5,-3)M(4,0)N(-6,2)P(5,-3.5)Q(0,5)R(6,2)·L·M·N·P·Q·R解:如图所示1、平面直角坐标系的概念在平面内画互相垂直,原点重合的两条数轴。2、由点写坐标①作垂线②找垂足3、由坐标找点①作垂线②找交点4、四象限点的坐标符号及坐标轴上点的坐标特征。小结教科书第68—69页习题7.1第2、3题布置作业