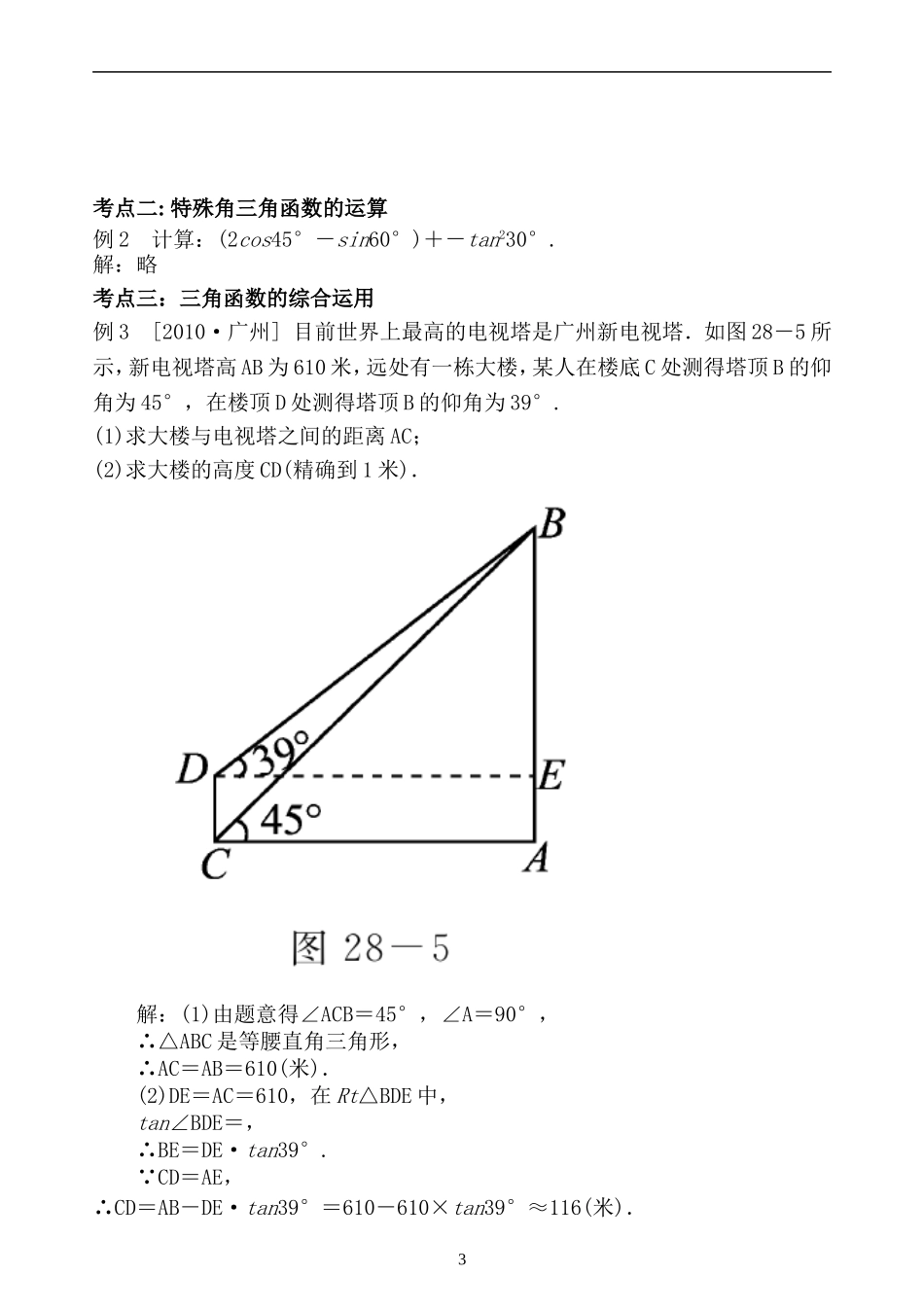
九年级数学《锐角三角函数》专题复习教学设计瓮安第五中学李景鸣【知识要点】一、三角函数的概念、特殊角的三角函数值、仰角、俯角的概念1、直角三角形ABC中,∠C=90º,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?(1)三边之间关系a²+b²=c²(勾股定理)(2)锐角之间关系∠A+∠B=90º(3)边角之间关系2.特殊角的三角函数值30°45°60°siaAcosAtanA3.仰角、俯角当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.二、直角三角形的性质1.直角三角形的两个锐角互余;2.直角三角形中斜边上的中线等于斜边的一半;(斜边上的中线正好把直角三角形分成两个等腰三角形)3.直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;(反之如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°)4.直角三角形中,两条直角边的平方和等于斜边的平方(称为勾股定理);1(反之,一个三角形中,有一条边的平方等于其它两边的平方和,那么它是直角三角形)三、直角三角形的其它特殊性质1.直角三角形中,如果两条直角边为a、b,斜边为c,斜边上的高为h,那么它们存在这样的关系:chab或cabh.2.直角三角形中,如果一个锐角等于30°,那么较长的直角边等于较短边的倍。3.在等腰直角三角形中,斜边是等于直角边的倍(斜边上的高正好是斜边的一半。)【典型例题】考点一:锐角三角函数的定义及性质例1如图28-2所示,∠BAC位于6×6的方格纸中,则tan∠BAC=________.2abchab=a30°caac=a45°考点二:特殊角三角函数的运算例2计算:(2cos45°-sin60°)+-tan230°.解:略考点三:三角函数的综合运用例3[2010·广州]目前世界上最高的电视塔是广州新电视塔.如图28-5所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(1)求大楼与电视塔之间的距离AC;(2)求大楼的高度CD(精确到1米).解:(1)由题意得∠ACB=45°,∠A=90°,∴△ABC是等腰直角三角形,∴AC=AB=610(米).(2)DE=AC=610,在Rt△BDE中,tan∠BDE=,∴BE=DE·tan39°.∵CD=AE,∴CD=AB-DE·tan39°=610-610×tan39°≈116(米).3答:大楼的高度CD约为116米.【巩固练习】1.如图1,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为______米.4