江西乐安一中高三数学 教案20代数 教案复习平面直角坐系和一次函数 教案几何圆的有关概念和定理VIP免费

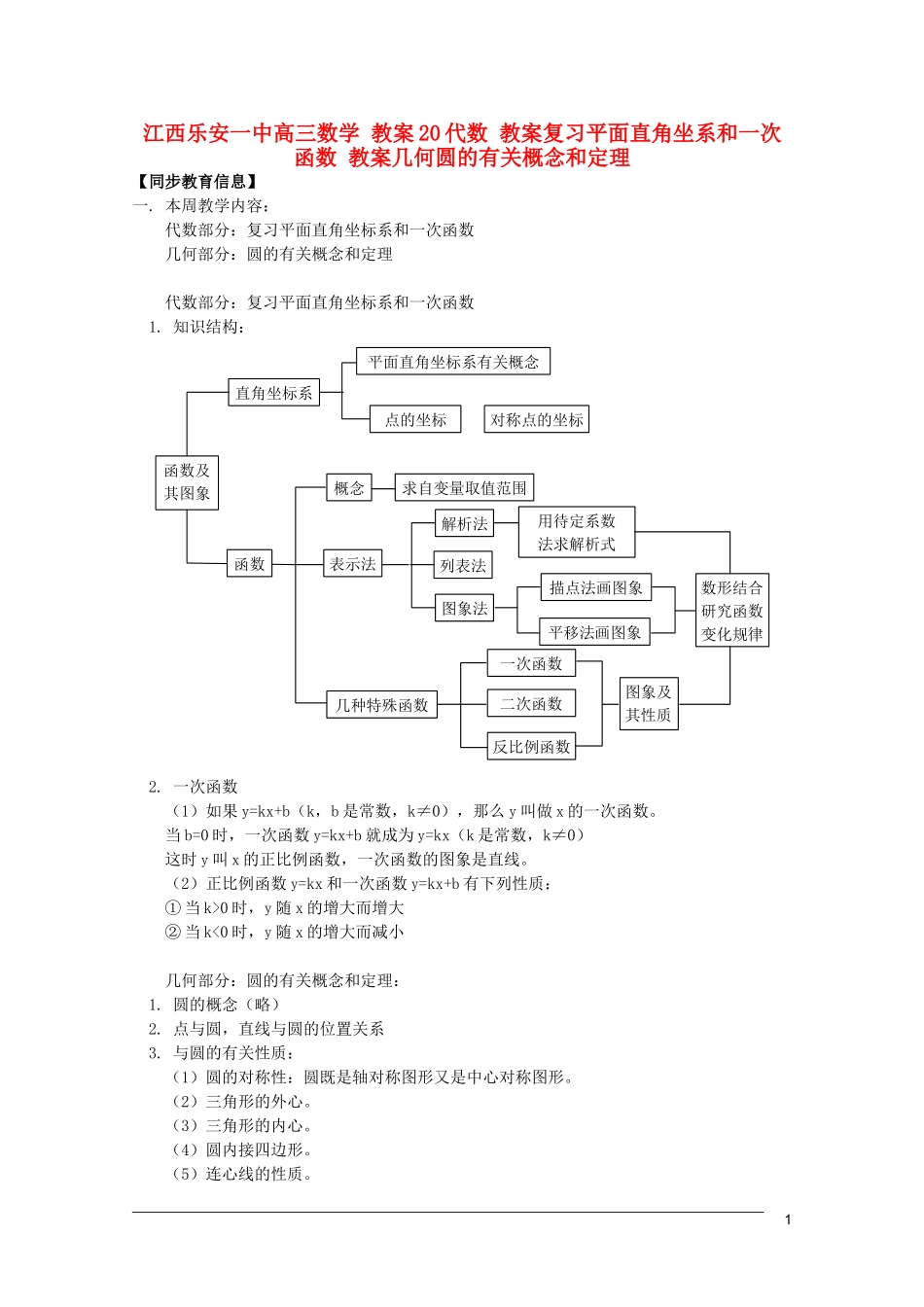
江西乐安一中高三数学教案20代数教案复习平面直角坐系和一次函数教案几何圆的有关概念和定理【同步教育信息】一.本周教学内容：代数部分：复习平面直角坐标系和一次函数几何部分：圆的有关概念和定理代数部分：复习平面直角坐标系和一次函数1.知识结构：平面直角坐标系有关概念点的坐标对称点的坐标直角坐标系函数及其图象函数概念求自变量取值范围解析法几种特殊函数列表法图象法用待定系数法求解析式描点法画图象平移法画图象数形结合研究函数变化规律一次函数二次函数反比例函数图象及其性质表示法2.一次函数（1）如果y=kx+b（k，b是常数，k≠0），那么y叫做x的一次函数。当b=0时，一次函数y=kx+b就成为y=kx（k是常数，k≠0）这时y叫x的正比例函数，一次函数的图象是直线。（2）正比例函数y=kx和一次函数y=kx+b有下列性质：①当k>0时，y随x的增大而增大②当k<0时，y随x的增大而减小几何部分：圆的有关概念和定理：1.圆的概念（略）2.点与圆，直线与圆的位置关系3.与圆的有关性质：（1）圆的对称性：圆既是轴对称图形又是中心对称图形。（2）三角形的外心。（3）三角形的内心。（4）圆内接四边形。（5）连心线的性质。14.与圆有关的定理：（1）垂径定理及推论（2）圆心角、弧、弦、弦心距之间的关系定理及推论（3）圆周角定理及推论（4）切线的判定与性质定理（5）切线长定理（6）弦切角定理及推论（7）相交弦定理及推论（8）切割线定理及推论二.重点、难点：重点：（1）对称点的坐标及一次函数的性质、画图象、求解析式。（2）圆的所有性质、定理及应用。难点：圆的有关综合性证明题。【典型例题】例1.已知：点A（0，0），B（3，0），点C在y轴上，且△ABC的面积是5，求C点坐标。分析：画图分析，点C在y轴上，但不知道点C在原点的上方还是在原点的下方，设点C坐标为（0，y），不能判断y与0的大小，因此要对y加绝对值，即|y|，并且在化简时要取正负。OBACC'(3,0)xy解：设点C坐标为（0，y）CAABSABACABC1212300||||y即12305103103||||yyy点的坐标为（，）或（，）C01030103例2.正比例函数与一次函数的图象如图，它们的交点坐标为A（4，3），B为一次函数与y轴交点，且OA=2·OB。（1）求正比例函数与一次函数解析式。（2）求△AOB的面积。2-3-23BO4xyA分析：根据交点为A（4，3），就可以确定正比例函数的系数，而确定一次函数的系数需要两个点。因此还需要求出B点坐标。由已知OA=2·OB，且OA可求，由勾股定理求出OA，即可求出B点坐标，而△AOB可看成以OB为底，以A点到y轴的距离4为高的三角形，则△AOB的面积也可求。解：（1）设正比例函数解析式为y=k1x，一次函数解析式为y=k2x+b过，得Akk()43343411正比例函数解析式为：yx34AAOAOB()43435222，，OBOA252点在轴上，且在轴下方，点坐标，Byx()052把，和，代入得ABykxb()()43052234521185222kbbkb一次函数解析式为yx11852（）2124125245SOBAOB例3.在平面直角坐标系内，一次函数y=kx+b(kb>0，b<0)的图象分别与x轴、y轴和直线x=4交于点A、B、C，直线x=4与x轴交于点D，四边形OBCD（O是坐标原点）的面积是10，若A点的横坐标是12，求这个一次函数的解析式。AOByCx=44xD分析：直线x=4是过x轴上的4这一点且与y轴平行的直线。3解：一次函数ykxbxAyB与轴交于点，，与轴交于点，()120()()0444，与直线交于点，bxCCkb又，kbbk000OBbCDkb，()4CDBOBOCD//，四边形是梯形，梯形OBCDSBOCDDOOBCD210bkb()42410整理得2521kb()又一次函数过点，ykxbA()1201202kb()252120112kbkbkb得所求一次函数解析式是yx12.例4.已知：在⊙O中，ABCD是圆内接四边形，过C点作DB的平行线交AB延长线于E。求证：BE·AD=BC·CDCAOBE123D证明：连结ACCEDB//231213又是圆的内接四边形ABCDCBEADCCBEADCB...