2.1.1平面2VIP免费

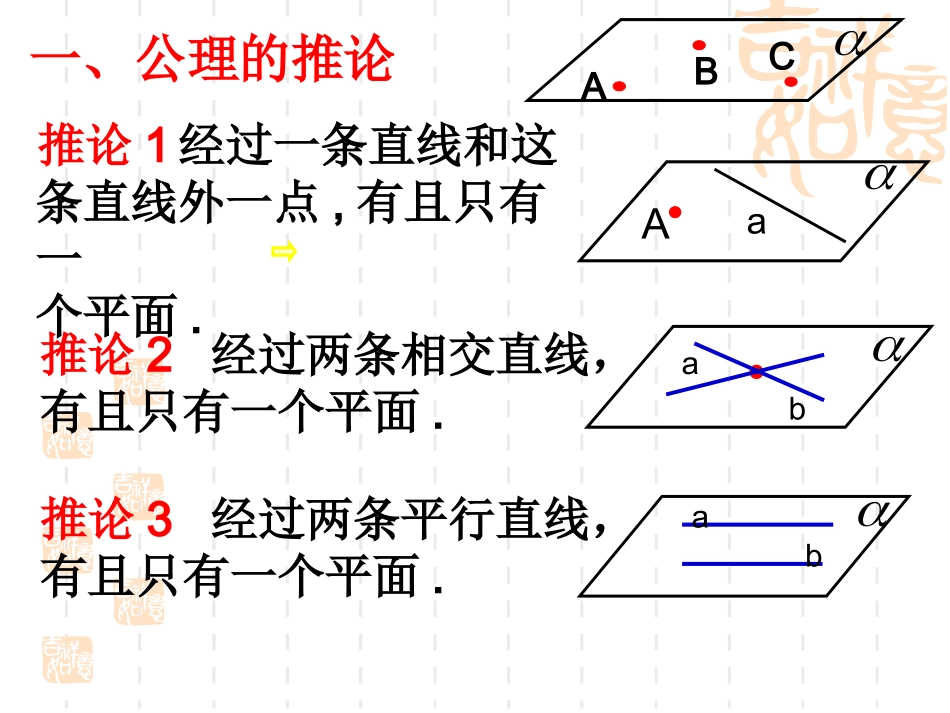
第二章第二章空间点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系推论1一、公理Aa经过一条直线和这条直线外一点,有且只有一个平面.推论2经过两条相交直线，有且只有一个平面.推论3经过两条平行直线，有且只有一个平面.baabABC的推论练习1、(1)两个平面的公共点的个数可能有......()(2)三个平面两两相交,则它们交线的条数……()(A)0(B)1(C)2(D)０或无数(A)最多4条最少3条(B)最多3条最少1条(C)最多3条最少2条(D)最多2条最少1条DB练习2、（１）判断题②两个平面可能只有一个公共点．③四条边都相等的四边形是菱形．×××（２）已知空间四点中，无三点共线，则可确定A．一个平面B．四个平面C．一个或四个平面D．无法确定平面的个数①若直线与平面有公共点，则称aa（３）平面α、β的公共点的个数多于两个，甲断定α、β一定重合，乙断定α、β至少有三个公共点，丙断定α、β至少有一条公共直线，丁断定α、β至多有一条公共直线，以上四个判断中，不正确的个数是A．0B．1C．2D．3（４）下列语句中正确的是A．平面ABCD是指平面四边形ABCD的四条边围起来的部分B．平面α的面积是10平方厘米C．100个平面重叠在一起比10个平面重叠在一起来得厚D．四边形不一定是平面图形顺次连结不共面的四点A、顺次连结不共面的四点A、4.空间四边形:二、共点、共线、共面问题空间中几个点或几条直线都在同一平面内即共面1、2、平面图形：构成图形的点都在同一平面内ABDC其中AC、BD叫空间四边形的对角线B、C、D，所组成的四边形B、C、D，所组成的四边形练习3、下列命题正确的是（）A.两组对边分别相等的四边形是平行四边形B.四条线段顺次首尾连接所构成的图形一定是平面图形；C.三条互相平行的直线一定共面；D.梯形是平面图形(2)公理2：“共点”、“共线”、“共面”问题(3)公理3,推论1、2、3:２、反证法１、理论依据：(1)公理1：判定两平证点、线共面的依据，确定平面也是作辅助面的依据面相交aAA,,A（“点共线”，“线共点”）判断或证明直线是否在平面内确定两个平面的交线，例1、△ABC在平面外,AB∩=Ｐ,BC∩=Ｑ，AC∩=Ｒ,求证:Ｐ、Ｑ、Ｒ三点共线.(共线问题)ABC又P∈证明:∵P∈AB且AB平面ABCQPR∴P∈平面ABC∴P∈平面ABC∩(公理3)设平面ABC∩=l则P∈l同理Q∈l且R∈l故P、Q、R三点共线于直线ll例2、如图：在四面体ABCD中，E,F分别是AB,BC的中点，G,H分别在CD,AD上,且DG:DC=DH:DA=1:m(m>2)求证：直线EH与FG,BD相交于一点ABCDEFGHP例3、已知棱长为a的正方体ABCD－A’B’C’D’中，M、N分别为CD、AD的中点。求证:M，N，A’，C’四点共面。NMC'D'B'A'DABC思考题正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状．3条直线相交于一点时：三条直线相交于一点,用其中的两条确定平面,最多可以确定3个。(1)3条直线共面时(2)每2条直线确定一平面时4条直线相交于一点时：三条直线相交于一点,用其中的两条确定平面,最多可以确定6个。(1)4条直线全共面时(2)有3条直线共面时(3)每2条直线都确定一平面时2个平面分空间有两种情况：两个平面把空间分成3或4个部分。(1)两平面没有公共点时(2)两平面有公共点时3个平面（2）（1）（3）（4）（5）3个平面把空间分成4，6，7或8个部分。若一条直线的两点在一个平面内，则这条直线上所有的点都在这个平面内,即:这条直线在这个平面内AABB小结:平面的基本性质公理1：作用:用于判定线在面内即:A∈且B∈ABABAaabABC作用:用于确定一个平面.ba且小结：公理2及其推论ab且a且b确定一平面.A∈aA和a确定一平面.A,B,C确定一平面.A,B,C不共线a且b确定一平面.a∥b公理3：若两个不重合平面有一个公共点，则它们有且只有一条过该点的公共直线。即:P∈且P∈l且P∈l｝｛P∈P∈lP∈l作用:用于证明点在线上或多点共线图形文字语言(读法)符号语言AaAaAaAAAA点在直线上点在直线外点在平面内点在平面外结论1:空间中点与线、点与面的位置关系Aa直线a在平面内记作：a直线a在平面外记作：a结论2：空间中线与面的位置关系强调:空间中点与线(面)只有∈和关系空间中线与面只有与的关系条件结论结论条件1条件2｝推导符号“”的使用：