三角形全等的条件(2)(SAS)VIP免费

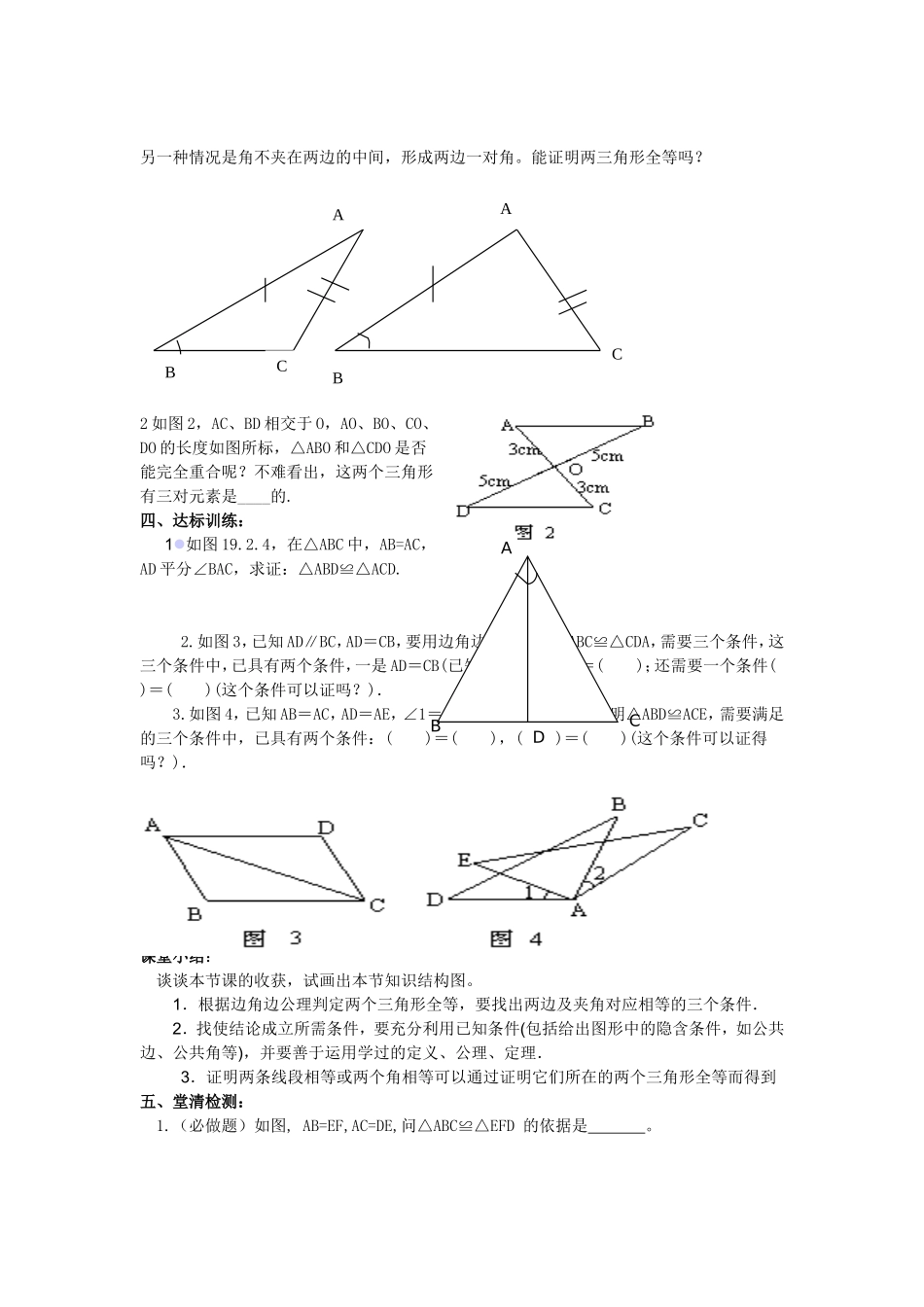
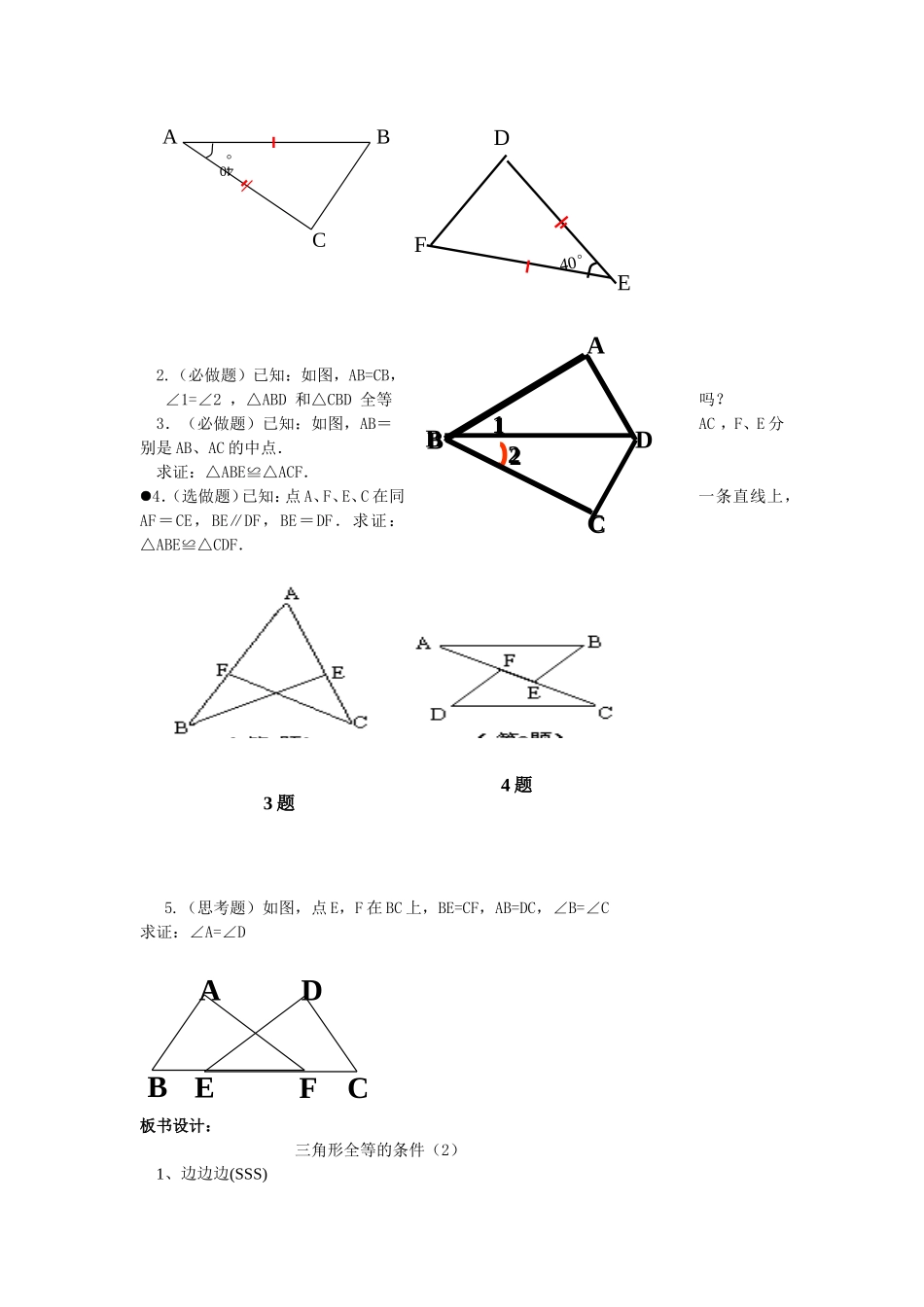
11．2三角形全等的条件（2）（SAS）教学目标：1、使学生掌握SAS定理，会运用SAS来判定两个三角形全等；2、通过判定全等三角形的学习，使学生初步认识事物之间的因果关系与相互制约关系，学习分析事物本质的方法；3、经历如何总结出全等三角形判定方法，体会如何探讨、实践、总结，培养学生的合作能力。重点难点：三角形全等的判定：SAS；对全等三角形的识别的理解和运用。教具准备：小黑板、三角尺教学过程：一、问题导入1．怎样的两个三角形是全等三角形？2．全等三角形的性质？3.上节课我们学习什么定理可以判定三角形全等？二、自主学习自学提纲：自学课本第6-8页内容，指出下图中各对全等三角形的对应边和对应角，并说明通过怎样的变换能使它们完全重合：图(1)中：△ABD≌△ACE，AB与AC是对应边；图(2)中：△ABC≌△AED，AD与AC是对应边．三.合作探究1.如果两个三角形有3组对应相等的元素，那么含有以下的四种情况：两边一角、两角一边、三角、三边。对于两边一角又有哪两种情形呢？AA(2)CDEDCBEB(1)边—角—边另一种情况是角不夹在两边的中间，形成两边一对角。能证明两三角形全等吗？2如图2，AC、BD相交于O，AO、BO、CO、DO的长度如图所标，△ABO和△CDO是否能完全重合呢？不难看出，这两个三角形有三对元素是____的.四、达标训练：1如图19.2.4，在△ABC中，AB=AC，AD平分∠BAC，求证：△ABD≌△ACD.2.如图3，已知AD∥BC，AD＝CB，要用边角边公理证明△ABC≌△CDA，需要三个条件，这三个条件中，已具有两个条件，一是AD＝CB(已知)，二是()＝()；还需要一个条件()＝()(这个条件可以证吗？)．3.如图4，已知AB＝AC，AD＝AE，∠1＝∠2，要用边角边公理证明△ABD≌ACE，需要满足的三个条件中，已具有两个条件：()＝()，()＝()(这个条件可以证得吗？)．课堂小结：谈谈本节课的收获，试画出本节知识结构图。1．根据边角边公理判定两个三角形全等，要找出两边及夹角对应相等的三个条件．2．找使结论成立所需条件，要充分利用已知条件(包括给出图形中的隐含条件，如公共边、公共角等)，并要善于运用学过的定义、公理、定理．3．证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到五、堂清检测：1.（必做题）如图,AB=EF,AC=DE,问△ABC≌△EFD的依据是。ACBACBBCDA2.（必做题）已知：如图，AB=CB，∠1=∠2，△ABD和△CBD全等吗？3．（必做题）已知：如图，AB＝AC，F、E分别是AB、AC的中点．求证：△ABE≌△ACF．4．（选做题）已知：点A、F、E、C在同一条直线上，AF＝CE，BE∥DF，BE＝DF．求证：△ABE≌△CDF．5.（思考题）如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C求证：∠A=∠D板书设计：三角形全等的条件（2）1、边边边(SSS)ABC40°D40°EFECDBFA3题4题BC121BCD2A2、边角边(SAS)课后反思：（本节课教学的得与失及感悟）