解析几何的几个常用结论及其应用VIP免费

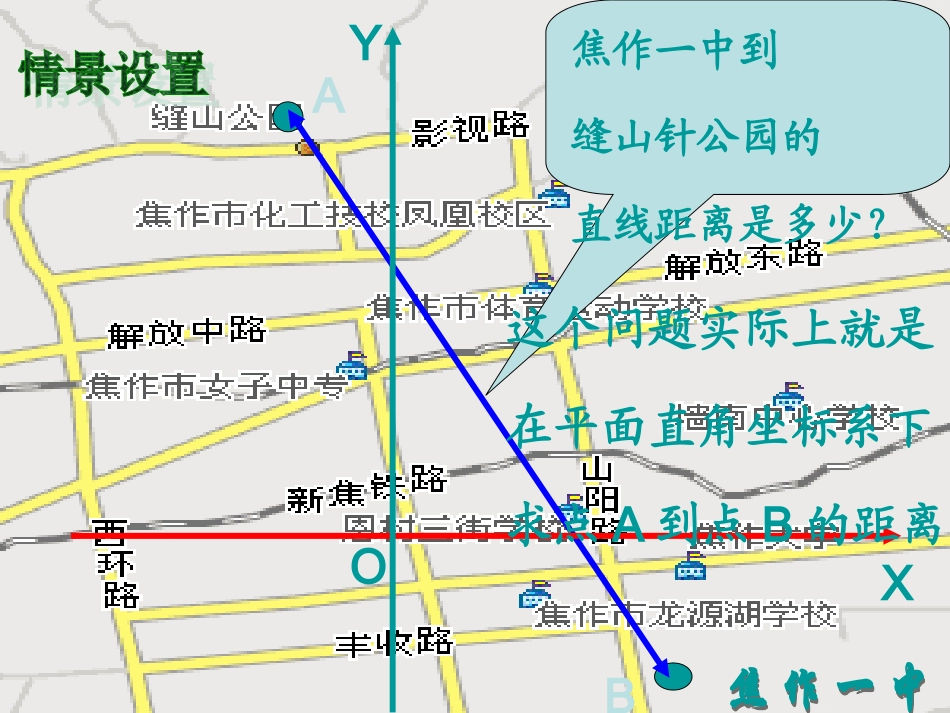
北师大版数学模块2第二章第一节第五课焦作一中到缝山针公园的直线距离是多少？XYOAB这个问题实际上就是在平面直角坐标系下求点A到点B的距离问题1：在初中，如何在数轴上求两点间的距离例如：如果A、B是x轴上两点，C、D是y轴上两点，它们坐标分别是XA、XB、YC、YD，那么|AB|、|CD|又怎样求？|AB|=|xB-XA|，|CD|=|YC-YD|XOAByDoC问题2：在平面直角坐标系下如何求两点间的距离？（1）在平面直角坐标系下，如果B(3,4),那么|OB|=?D问题2：在平面直角坐标系下如何求两点间的距离？（2）在平面直角坐标系下，A(-5,-2),B(3,4),那么|AB|=?C(3,-2)显然，在Rt△ACB中|AC|=3-(-5)=8|BC|=4-(-2)=6由勾股定理得：2222||||||8610ABCABC问题2：在平面直角坐标系下如何求两点间的距离？一般地，若两点A,B的坐标分别是A(X1,Y1),B(X2,Y2)则两点A，B间的距离？C21|AC|=|X|X21|BC|=|Y|Y过A点作Y轴的垂线，过B点作X轴的垂线，两垂线的交点为C(X2,Y1)(X2,Y1)222121||()()ABxxyy一般地，若两点A,B的坐标分别是A(X1,Y1),B(X2,Y2)则有两点A，B间的距离公式特别地：当ABX∥轴时，X1＝X2，|AB|=|Y2-Y1|当CDY∥轴时，Y1＝Y2，|AB|=|X2－X1|例1求下列两点间的距离（1）A(-1,0)B(2,3)(2)A(4,3)B(7,-1)例2已知△ABC的三个顶点是A(－1，0),B(1，0),C(),试判断△ABC的形状。13,22解：22||(21)(30)991832AB解：22||(74)(13)916255AB跟踪练习方法1：距离公式方法2：斜率法方法3：平面几何法221313||1224BC＋解：因＝（1－）（）＝＝2233||2,||()()322ABAC222||||||ACBCAB有＋＝所以△ABC为直角三角形解：设直线AC的斜率为K1,直线BC的斜率为K2则1303213(1)2K230321312K121KKACBC所以＝－，即则△ABC为直角三角形D解:过C作CDAB⊥，垂足为D,3||2CD3||2AD1||2BD33CDBDADCD所以则有Rt△ADC∽Rt△CDBABCD那么90BCDB又因＋90C所以则有△ABC为直角三角形例3：△ABC中，D是BC边上任意一点（D与B，C不重合）且求证：△ABC为等腰三角形22||||||||ABADBDDCBCADXY（0，a）(b,0)(d,0)(c,0)o解：AOBC,⊥垂足为O，以BC所在的直线为X轴，以OA所在的直线为Y轴，建立直角坐标系。因为，所以，由距离公式得：22||||||||ABADBDDC2222()()badadbcd(db)(bd)(db)(cd)即db0又bdcd故bc即所以，O为线段BC的中点，那么|AB|=|AC|,即△ABC为等腰三角形。设A(0,a),B(b,0),C(c,0)D(d,0)OABCDXYOABCDXY方法2：以BC所在直线为X轴，以BC边的中垂线为Y轴，建立直角坐标系。方法3:以B为坐标原点，以BC所在直线为X轴，建立直角坐标系。1，求下列两点的距离2，已知点A(x,-5)和B(0,10)的距离为17，求X的值。1A30B202C21D333E2F2,)22（）(-,)(,)()(,)(2,-5)()(,-)((,2),(2,3),(1,1),||||PaQMPQPM且1.已知点，求a的值3，求函数228201yxxx的最小值(1,2)AB，（5，2），2，已知若P求点的坐标|PA|=10||2PB，