3.1.2导数的概念VIP免费

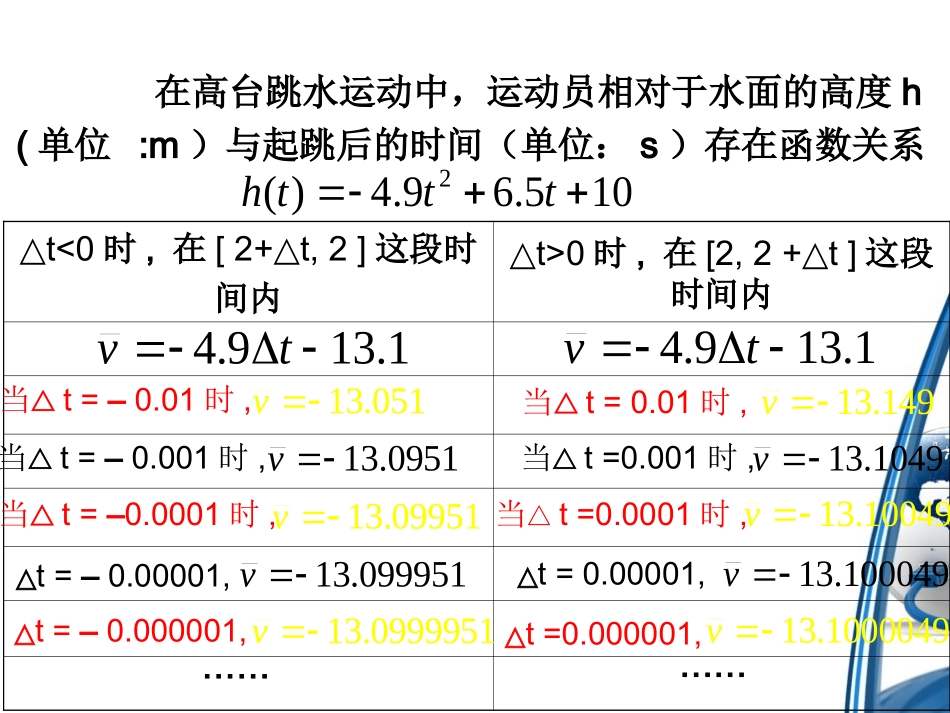
3.1.2导数的概念晋城中学田智慧引入：•在高台跳水运动中,平均速度不能反映她们在这段时间里运动状态，需要用描述运动状态。我们把物体在某一时刻的速度称为又如何求瞬时速度呢?瞬时速度瞬时速度△t<0时,在[2+t,2]△这段时间内△t>0时,在[2,2+t]△这段时间内1.139.4tv1.139.4tv051.13v当△t=–0.01时,149.13v当△t=0.01时,0951.13v当△t=–0.001时,1049.13v当△t=0.001时,09951.13v当△t=–0.0001时,10049.13v当△t=0.0001时,099951.13v△t=–0.00001,100049.13v△t=0.00001,0999951.13v△t=–0.000001,1000049.13v△t=0.000001,…………在高台跳水运动中，运动员相对于水面的高度h(单位:m）与起跳后的时间（单位：s）存在函数关系105.69.4)(2ttth当△t趋近于0时,即无论t从小于2的一边,还是从大于2的一边趋近于2时,平均速度都趋近与一个确定的值–13.1.1.13)2()2(lim0ththt从物理的角度看,时间间隔|△t|无限变小时,平均速度就无限趋近于t=2时的瞬时速度.因此,运动员在t=2时的瞬时速度是–13.1.v表示“当t=2,t△趋近于0时,平均速度趋近于确定值–13.1”.v从2s到(2+t)s△这段时间内平均速度tthv9.41.13思考:1.运动员在某一时刻t0的瞬时速度怎样表示?5.68.9)5.68.99.4(lim)5.68.9()(9.4lim)()(lim000020000ttttttttthtthtttxyxxfxxfxxlimlim0000)(2.函数f(x)在x=x0处的瞬时变化率怎样表示?定义:函数y=f(x)在x=x0处的瞬时变化率是xyxxfxxfxxlim)()Δ(lim0000称为函数y=f(x)在x=x0处的导数,记作.)()Δ(lim)(0000xxfxxfxfx即)(0xf0|xxy或。其导数值一般也不相同的值有关，不同的与000)(.1xxxf的具体取值无关。与xxf)(.20一概念的两个名称。瞬时变化率与导数是同.3说明：)(xf0x0xxyxy0x（1）函数在点处可导，是指时，有极限．如果不存在极限，就说函数在处不可导，或说无导数．点x是自变量x在0x处的改变量，0x，而y是函数值的改变量，可以是零．（2）例1.(1)求函数y=x2在x=1处的导数.三．典例分析解：第一步先求2221)1()1()1(yxxxfxfxx2y2lim0xyx第二步第三步求函数y=f(x)的导数的一般方法:1.求函数的改变量2.求平均变化率3.求值);()(00xfxxfy.lim)(00xyxfx;)()(00xxfxxfxy一差、二比、三极限求函数f(x)=-x2+x在x=-1附近的平均变化率，并求出在该点处的导数．22231)1()1()1()1()1(yxxxxfxf）（xx3y3)3(limlim00xxyxx解：2.如果质点A按s=2t3运动，则在t=3s时的瞬时速度是（）A6B18C54D81C_________)()(,3)(.3000h0limhhxfhxfxf则若-61221)()21(lim)()21(lim2-(.40000000hxfhxfhxfhxfxfhh，则）若1)21(21)()21(000limhxfhxfh原式改正：注明：分子中自变量的增量与分母中的增量必须保持一致想一想？小结：2、求导数的一般步骤：（1）求函数的增量Δy=f(x0+Δx)-f(x0)(2)求平均变化率（3）求极限yx'00()limxyfxx1、导函数的定义作业：教材p80习题3、4、5