三角函数的图像(蒲东风编)VIP免费

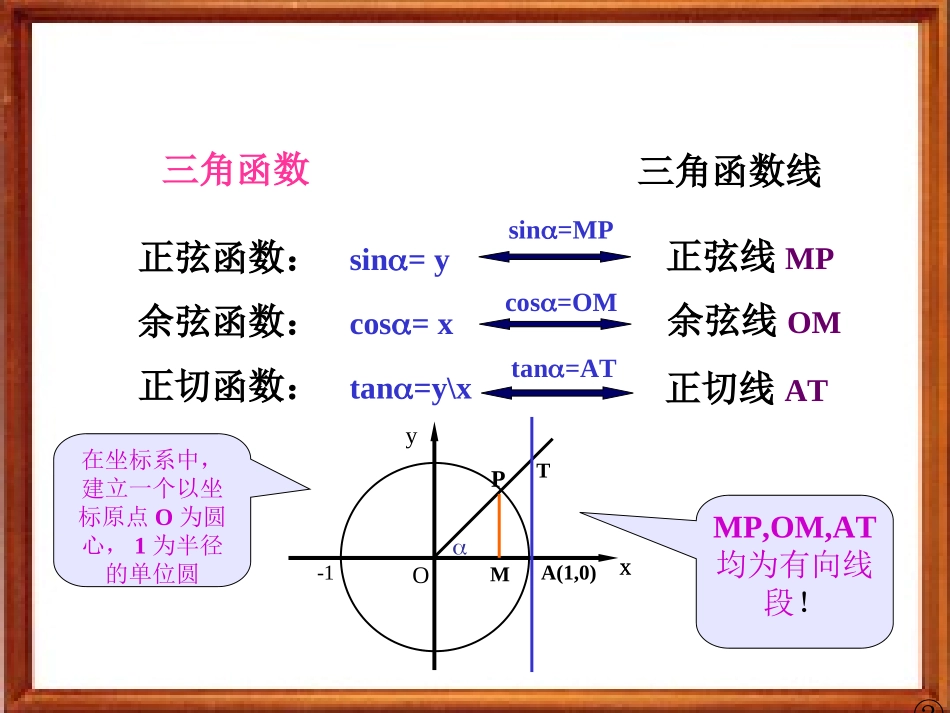
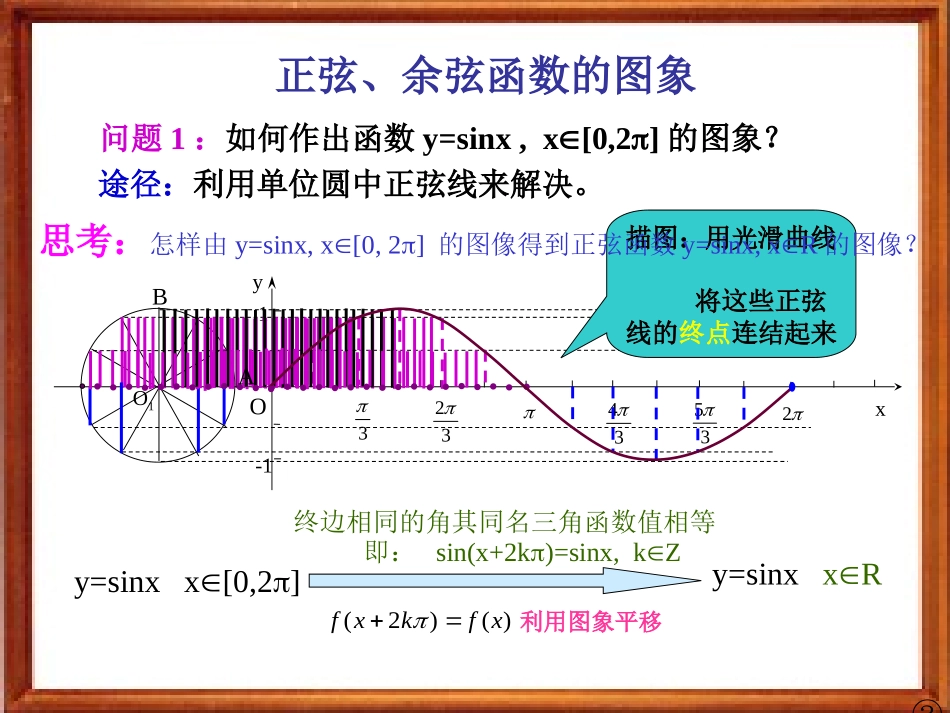
三角函数中的最值问题高一数学组主讲：代希明①三角函数三角函数线正弦函数：sin=y余弦函数：cos=x正切函数：tan=y\x正切线ATyxO-1PMA(1,0)Tsin=MPcos=OMtan=ATMP,OM,AT均为有向线段！正弦线MP余弦线OM在坐标系中，建立一个以坐标原点O为圆心，1为半径的单位圆②正弦、余弦函数的图象问题1：如何作出函数y=sinx,x[0,2]的图象？途径：利用单位圆中正弦线来解决。y=sinxx[0,2]O1Oyx33234352-11y=sinxxR终边相同的角其同名三角函数值相等即：sin(x+2k)=sinx,kZ)()2(xfkxf描图：用光滑曲线将这些正弦线的终点连结起来利用图象平移AB③思考：怎样由y=sinx,x[0,2]的图像得到正弦函数y=sinx,xR的图像？正弦、余弦函数的图象x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322④xo1-1222x6yo--12345-2-3-41正弦、余弦函数的图象余弦函数y=cosx的图象正弦函数y=sinx，xR的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同问题2:联系学过的诱导公式，你能否以正弦函数的图像为基础，通过适当的图形变换得到余弦函数的图像？⑤正弦、余弦函数的图象yxo1-122322思考:在函数y=sinx,x[0,2]的图像上，那些点是关键点？(0,0)(,1)2(,0)(,-1)23(2,0)五点作图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)⑥正弦、余弦函数的图象随堂练习1：用“五点法”画出函数y=sinx，x[0,2]的简图：xsinx22302010-10o1yx22322-1y=sinx，x[0,2]步骤：1.列表2.描点3.连线⑦正弦、余弦函数的图象作图的过程比较烦琐作出的图象比较精确作图的过程比较简单不精确感悟：两种方法都能作出正弦函数的图像，他们各有什么优缺点？用正弦线作正弦函数图像优点：缺点：用五点法作正弦函数图像优点：缺点：⑧正弦、余弦函数的图象思考:在作函数y=cosx,x[0,2]的图像时，又应抓住那些关键点？yxo1-122322(0,1)(,0)2(,-1)(,0)23(2,1)(0,1)(,0)2(,-1)(,0)23(2,1)五点法——y=cosx，x[0,2]⑨正弦、余弦函数的图象例1：用“五点法”画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线y=sinx，x[0,2]⑩正弦、余弦函数的图象例2：用“五点法”画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]⑾正弦、余弦函数的图象随堂练习2：用"五点法”画出函数y=cosx，x[,]的简图：223o1yx22322-12y=cosx，x[,]223xcosx100-1022302⑿正弦、余弦函数的图象x6yo--12345-2-3-41正弦曲线x6yo--12345-2-3-41余弦曲线⒀正弦、余弦函数的图象小结1.正弦曲线、余弦曲线的作法：几何画法五点法2.作图时注意与诱导公式、三角函数线等知识的联系yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]3.作图时要善于利用图像的变换课本：P46习题1.4A组T1作业⒁正弦、余弦函数的图象能力提升：画出函数y=1+2cos2x，x[0,]的简图：10-10131-113443y=1+cos2x，x[0,]⒂2xxcos2x1+cos2x02223202434yx1-1o3同学们,今天的课就上到这里，望大家能有所收获；课后别忘了复习巩固并及时完成作业！再见呵︵呵同学们