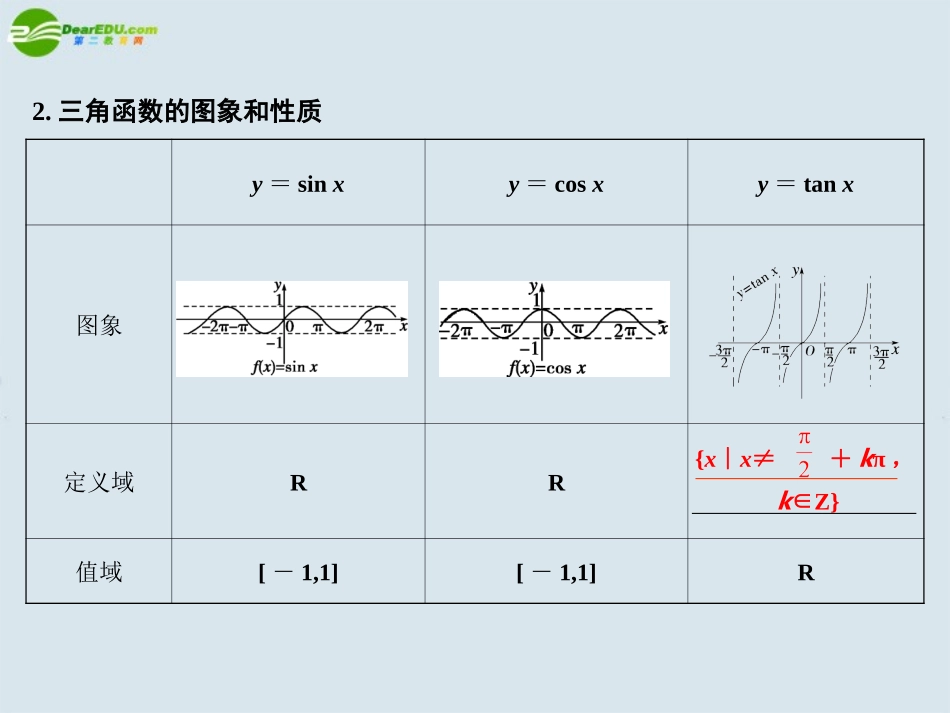
能画出y=sinx,y=cosx,y=tanx的图象,了解三角函数的周期性/理解正弦函数、余弦函数在区间[0,2π]的性质(如单调性、最大和最小值与轴交点等)/理解正切函数在区间(-)内的单调性/了解函数y=Asin(ωx+φ)的物理意义/能画出y=Asin(ωx+φ)的图象,了解参数A,ω,φ对函数图象变化的影响/了解三角函数是描述周期变化现象的重要函数模型/会用三角函数解决一些简单实际问题3.4三角函数的图象与性质1.用五点法作正弦函数和余弦函数的简图正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0)(,1)(π,0)(,-1)(2π,0)余弦函数y=cosx,x∈[0,2π]的五个关键点是:(0,1)(,0)(,0)(2π,1)(π,-1)2.三角函数的图象和性质y=sinxy=cosxy=tanx图象定义域RR值域[-1,1][-1,1]R{x∣x≠+kπ,k∈Z}奇偶性奇函数奇函数周期性最小正周期为2π最小正周期为2π最小正周期为单调性在(-+2kπ,+2kπ)k∈Z函数单调,在(+2kπ,+2kπ)k∈Z函数单调递减在(-π+2kπ,2kπ)k∈Z内函数单调,在(2kπ,2kπ+π)k∈Z时函数单调递减在开区间(-+kπ,+kπ)k∈Z,函数单调递增递增递增偶函数π3.周期性一般地,对于函数f(x),如果存在一个非零常数T,对定义域内的任意一个x值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,T叫做这个函数的周期.对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的.函数y=Asin(ωx+φ),x∈R及函数y=Acos(ωx+φ),x∈R(其中A、ω、φ为常数,且A≠0,ω>0)的周期T=.最小正周期1.函数y=|sinx|的一个单调增区间是()解析:函数y=|sinx|的图象如右图所示:可观察出函数y=|sinx|在(π,)上递增.答案:C2.将函数y=sinωx(ω>0)的图象按向量a=(-,0)平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是()A.y=sin(x+)B.y=sin(x-)C.y=sin(2x+)D.y=sin(2x-)解析:函数y=sinωx(ω>0)的图象按向量a=(-,0)平移,平移后图象对应的解析式是答案:C3.已知函数f(x)=(sinx+cosx)-|sinx-cosx|,则f(x)的值域是()答案:C4.若f(x)=asin(x+)+3sin(x-)是偶函数,则a=________.答案:-3由函数y=sinx的图象通过变换得到y=Asin(ωx+φ)的图象,主要有两种途径:“先平移,后伸缩”与“先伸缩,后平移”.【例1】为了得到函数y=sin(2x-)的图象,可以将函数y=cos2x的图象()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度答案:B变式1.函数f(x)=|sinx+cosx|的最小正周期是()A.B.C.πD.2π解析:f(x)=|sinx+cosx|=,结合f(x)的图象可知f(x)的最小正周期为π.答案:C可由函数y=Asin(ωx+φ)的最值求A;利用其周期(或半个周期,四分之一周期等)求ω;由五点作图的过程求φ.【例2】由下列f(x)=Asin(ωx+φ)(A>0,0≤φ<)的一段图象确定各图象对应的f(x)的表达式.变式2.下列函数中,图象的一部分如图所示的是()A.y=sin(x+)B.y=sin(2x-)C.y=cos(4x-)D.y=cos(2x-)答案:D形如y=asinx+bcosx,y=asin2x+bsinxcosx+ccos2x等函数可化为y=Asin(ωx+φ)+k的形式,进而可解决三角函数的图象和性质等问题.【例3】设函数f(x)=cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为.(1)求ω的值;(2)如果f(x)在区间上的最小值为,求a的值.变式3.设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx,sin2x+m)(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间;(2)当x∈[0,]时,-4