直线与双曲线(1)VIP免费

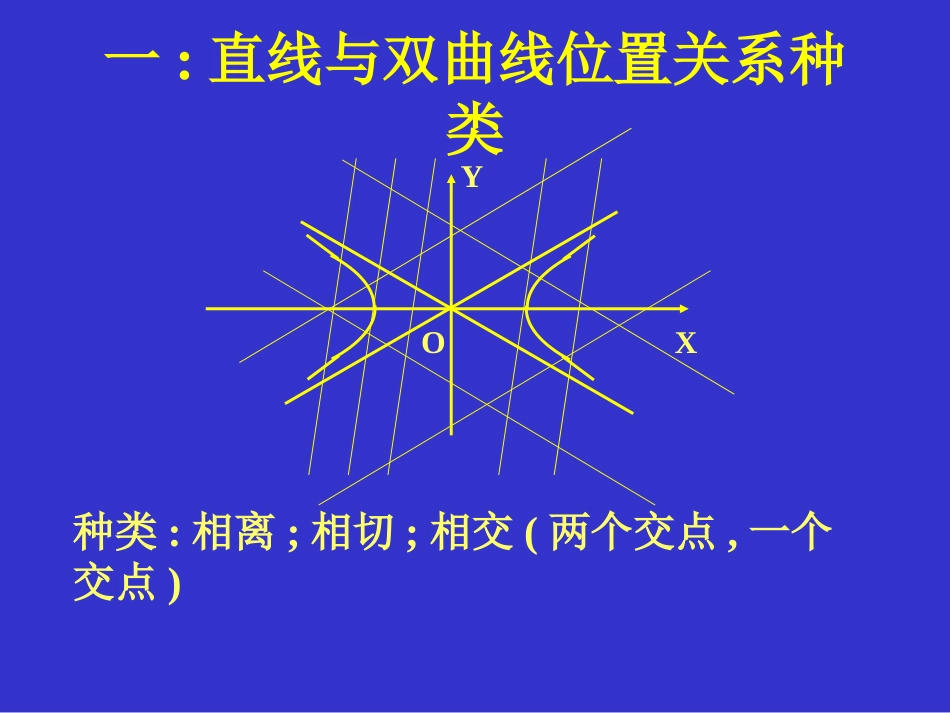
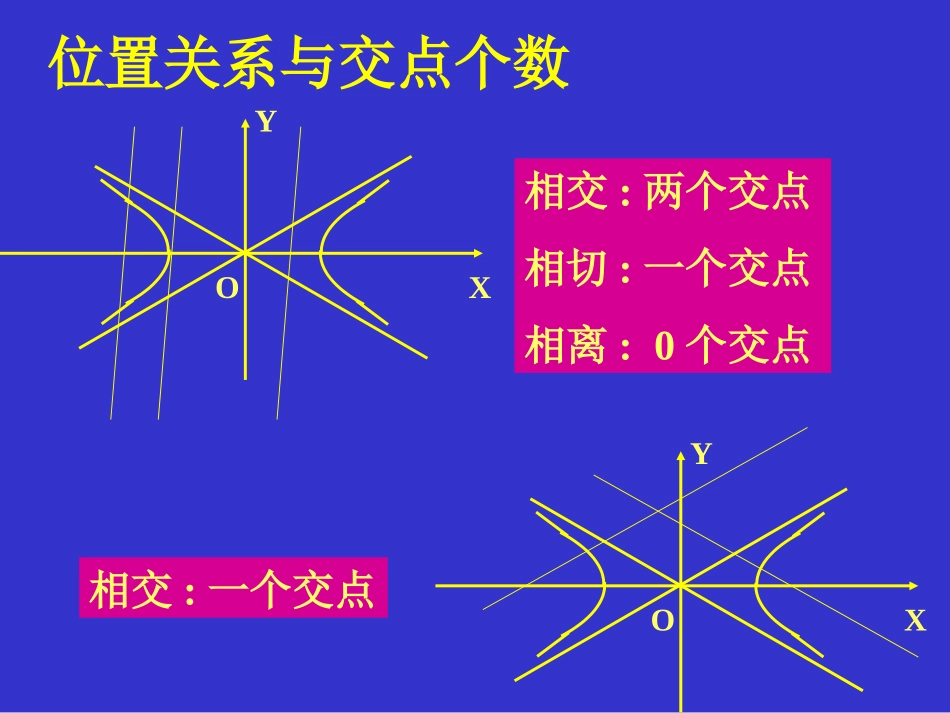
直线与双曲线一:直线与双曲线位置关系种类XYO种类:相离;相切;相交(两个交点,一个交点)位置关系与交点个数XYOXYO相交:两个交点相切:一个交点相离:0个交点相交:一个交点总结两个交点一个交点0个交点相交相切相交相离交点个数方程组解的个数有没有问题?天哪!=0一个交点?相切相交>0<00个交点两个交点相离相交[1]0个交点和两个交点的情况都正常,那么,依然可以用判别式判断位置关系[2]一个交点却包括了两种位置关系:相切和相交(特殊的相交),那么是否意味着判别式等于零时,即可能相切也可能相交?实践是检验真理的唯一标准!请判断下列直线与双曲线之间的位置关系[1]1169:,3:22yxcxl[2]1169:,134:22yxcxyl相切相交回顾一下:判别式情况如何?一般情况的研究1:,:2222byaxcmxabyl显然,这条直线与双曲线的渐进线是平行的,也就是相交.把直线方程代入双曲线方程,看看判别式如何?根本就没有判别式!唉!白担心一场!当直线与双曲线的渐进线平行时,把直线方程代入双曲线方程,得到的是一次方程,根本得不到一元二次方程,当然也就没有所谓的判别式了。结论：判别式依然可以判断直线与双曲线的位置关系！好也!=0一个交点相切>0<00个交点两个交点相离相交判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐进线平行相交（一个交点）计算判别式>0=0<0相交相切相离判断下列直线与双曲线的位置关系11625:,154:]1[22yxcxyl相交(一个交点)11625:,145:]2[22yxcxyl相离例1.已知直线l：y=ax+1与双曲线交于A、B两点⑴求a的取值范围.⑵若直线l过左焦点，求弦AB的长.F1ABxyo22x1y(2)左焦点（,0)22:12lyx设A(x1,y1),B(x2,y2）22221224021yxxxxy4222121xxxx22121214ABkxxxx211224426解题回顾：求直线与双曲线相交的弦长的方法（1）利用|AB|=和韦达定理求弦长.（2）若直线过焦点，则可考虑利用第二定义；在应用时要区分两种情形.2121xxka、如果两交点在同一支上，那么|AB|=|AF1|+|BF1|b、如果两交点在两支上，那么|AB|=||AF1|-|BF1||F1ABxyOxyF1ABO练习1：1.若例1中，求ΔAOB的面积.2.两条渐近线方程且截直线x-y-3=0所得弦长为的双曲线方程为.20xy83323ayxo例2：已知双曲线的方程为⑴求以P(2,1)为中点的弦MN所在的直线方程.⑵试问是否存在被点B(1,1)平分的弦？如果存在，求出弦所在的直线方程，如果不存在说明理由.2212yx)1,2(PNM分析：（1）k不存在时显然不合题意;1(2)ykx221(2)12ykxyx22222124430kxkkxkkM(x1,y1),M(x2,y2）22(12)12222kkkxx4k所求的直线方程为4x-y-7=0设所求直线方程为：yxo例2.已知双曲线的方程为⑴求以P(2,1)为中点的弦MN所在的直线方程.⑵试问是否存在被点B(1,1)平分的弦？如果存在，求出弦所在的直线方程，如果不存在说明理由.2212yx)1,1(B)1,2(PNM（2）假设存在这样的弦，221(1)12ykxyx2222222230kxkkxkk22221222kkkxx2k2224301642380kxx当时，为此时，∴不存在这样的弦k不存在显然不合题意设弦所在的直线方程为：)1(1xky并且交双曲线于C(x1,y1),D(x2,y2）解题回顾：求以定点为中点的弦所在的直线方程的基本思路:（1）通过联列方程组，消去一个变量转化成一元二次方程，结合根与系数的关系求斜率.（2）利用点差法求斜率.解法要领：设而不求，两式相减.（3）点差法求方程要注意检验:如果点在双曲线内部（图中的阴影部分），那么以该点为中点的弦一定存在.如果点在双曲线外部（图中的另外部分），那么以该点为中点的弦不一定存在，必须检验.42-2-4-5510xoy练习2.已知双曲线中心在原点，且一个焦点为F(，0)，直线y=x-1与其相交于M、N两点，MN的中点的横坐标为，则此双曲线的方程为（）23722.134xyA22.143xyB22.152xyC22.125xyD思考题：(2002全国)设A、B是双曲线上的两点，N(1,2)是线段A...