山西省原平市第一中学2012-2013学年高一数学-平面几何中的向量方法导学案VIP免费

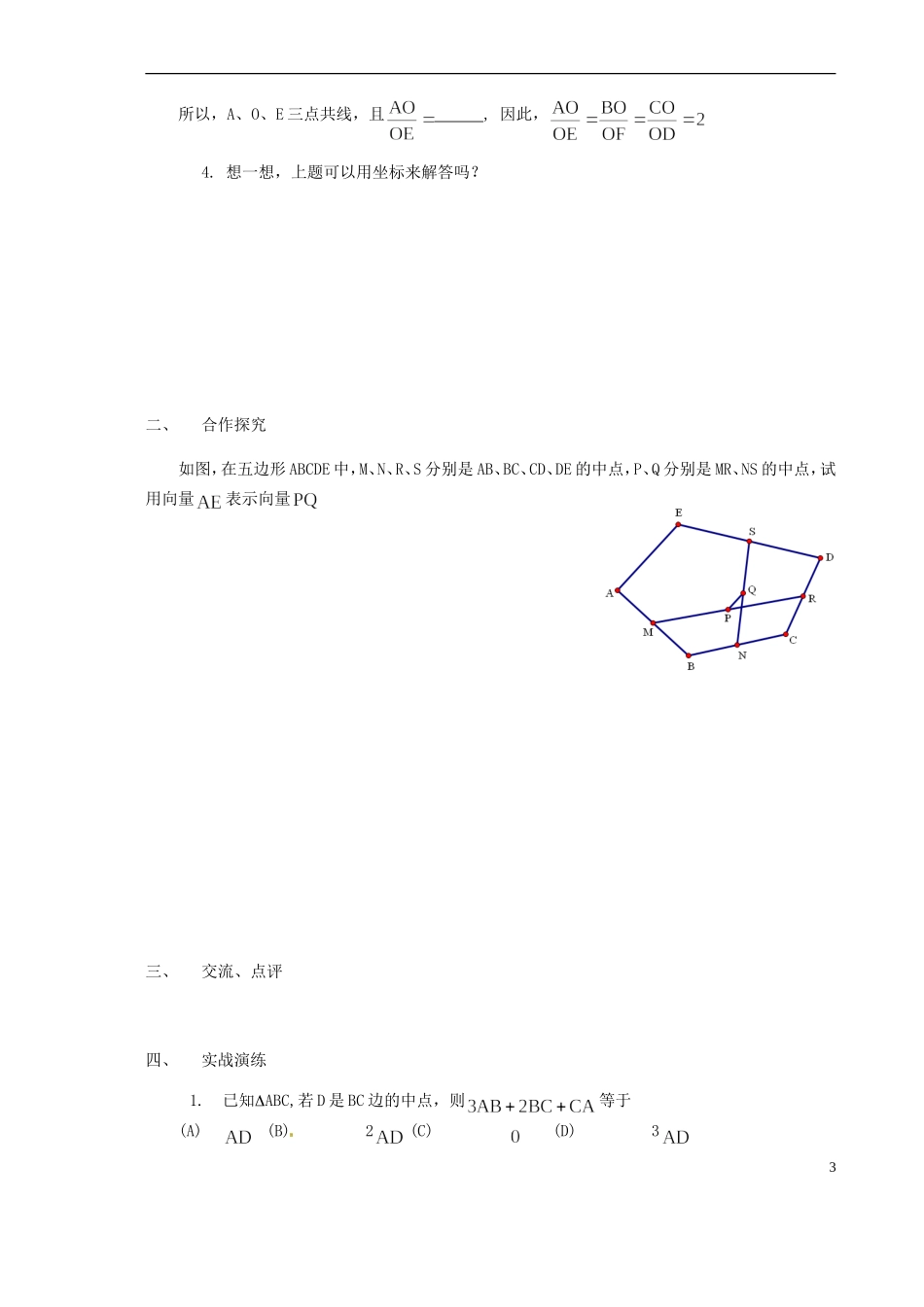
山西省原平市第一中学2012-2013学年高一数学平面几何中的向量方法导学案(2)发展学生的运算能力和解决问题的能力。一、文本研读问题一：请阅读P109开始到P110例2前的内容，回答下列问题。1.在向量中，若，则=,2.用向量方法解决平面几何问题的“三步曲”是：(1)(2)(3)问题二：请阅读P110例2以及下面的解答，回答下列问题。例2的坐标解法：如图，建立直角坐标系记B(b,0),D(a,c),则=(a,c)(b,0)=(ab,c)设=(x,y)由RAC有//于是(ab)ycx=0①由E为AD的中点有E于是又(xb,y)1由RBE有//于是②联解①②组成的方程组，得x=,y=所以，以下略。1.在符号运算下，向量平行时，通常用：非零向量与平行，当且仅当有唯一实数，使2.在坐标运算下，向量平行时，通常用：若=(x1,y1),=(x2,y2)，则//的充要条件是3.请补全下面的解答。题：如图，D,E,F分别为ABC的边AB,BC,CA的中点，BF与CD相交于一点O,设。(1)用表示向量(2)求证：A、O、E三点共线，且解：(1)由D,F分别为AB,CA的中点，得DEBC于是OFD∽OBC则，由数乘定义，因此，(2)于是=2所以，A、O、E三点共线，且,因此，4.想一想，上题可以用坐标来解答吗？二、合作探究如图，在五边形ABCDE中，M、N、R、S分别是AB、BC、CD、DE的中点，P、Q分别是MR、NS的中点，试用向量表示向量三、交流、点评四、实战演练1.已知ABC,若D是BC边的中点，则等于(A)(B)2(C)(D)332.若O为ABC所在平面内一点，且满足，则一定有(A)(B)(C)(D)3.已知A(2,3),B(4,3),点P在线段AB的延长线上，且,求点P的坐标。4.已知：三角形的三条中线交于一点，这点称为该三角形的重心；三角形的三条高线交于一点，这点称为该三角形的垂心；三角形的三条角平分线交于一点，这点称为该三角形的内心；三角形的三条边的垂直平分线交于一点，这点称为该三角形的外心；请指出在下列条件下，O是ABC的什么“心”？(1).(2).五、能力提升阅读下面的解答，并用坐标法给出另一种证明。题：证明三角形的三条高线交于一点。已知：如图，AD、BE、CF分别为ABC的三条高线。求证：AD、BE、CF交于一点。证明：设BE与CF的交点为M并记则因为BMAC,CMAB,于是则化简得即则AMBC,又ADBC因此MAD所以，AD、BE、CF交于一点。4六、小结与反馈5